Geometry Nets Worksheet

Geometry nets worksheets provide a valuable resource for students learning about the different types of two-dimensional figures and their corresponding three-dimensional counterparts. With a focus on visual learning, these worksheets offer a variety of exercises and activities centered around manipulating and assembling nets to form solid shapes. Designed specifically for middle school and high school students studying geometry, these worksheets offer a practical and engaging way to reinforce mathematical concepts related to spatial reasoning and visualization.

  Cube Volume Worksheets 5th Grade Math

---

  Nets Geometry Printable Worksheets

---

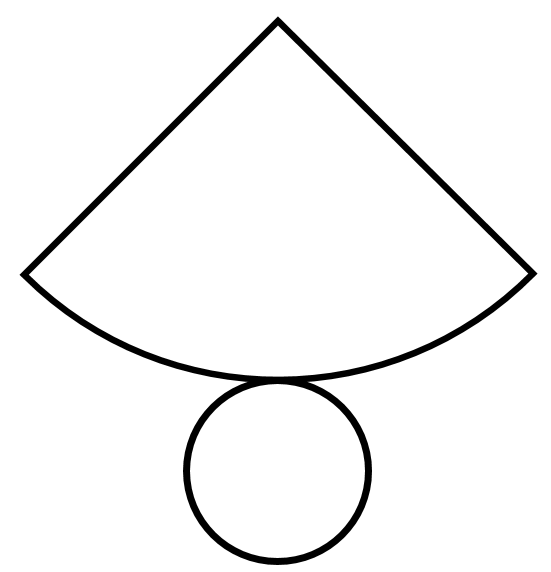
  Cone Net Shape

---

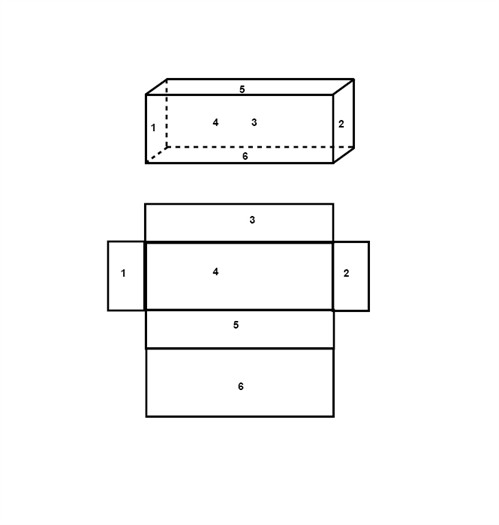
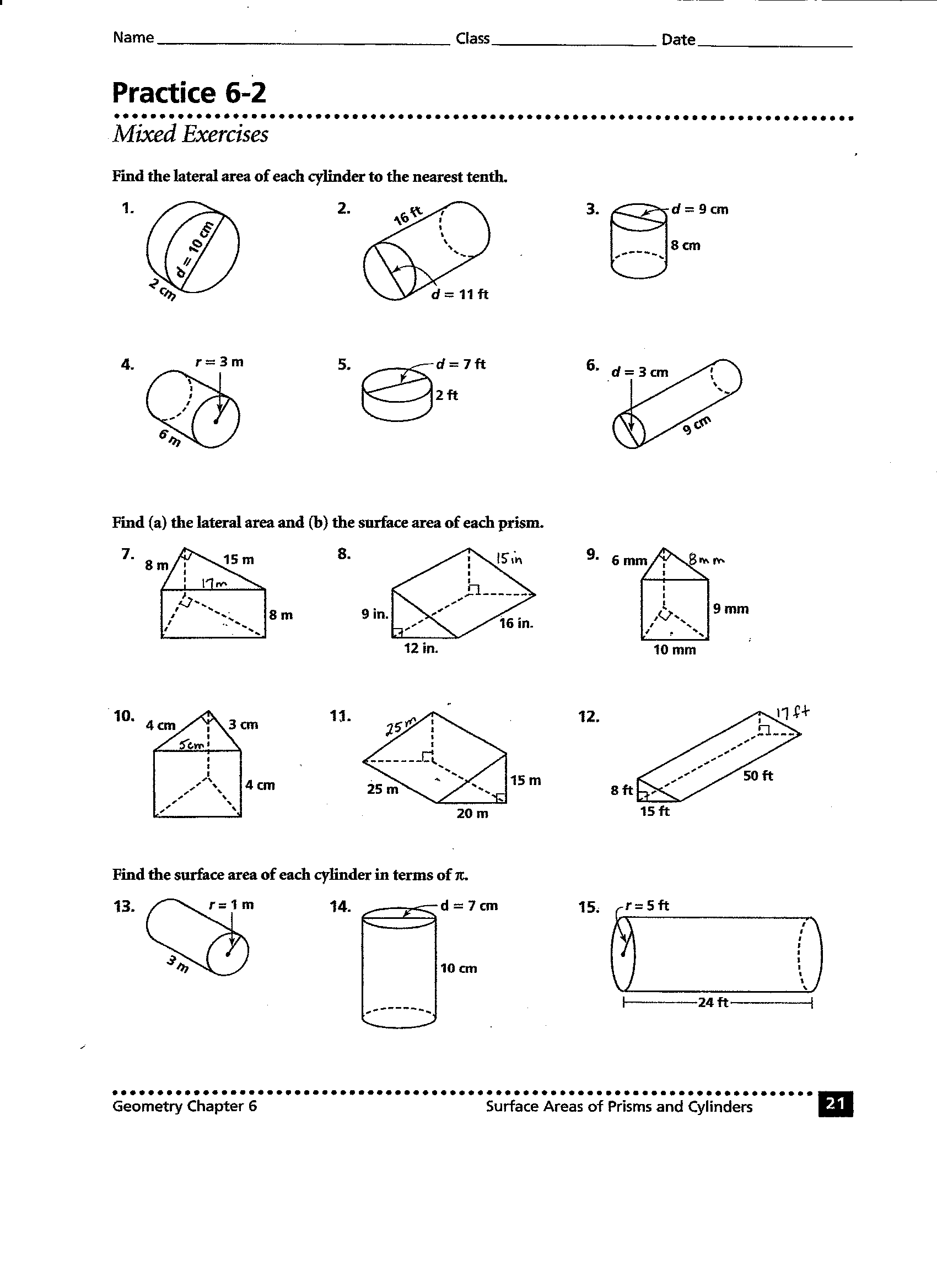
  A of a Rectangular Prism and Cube Nets

---

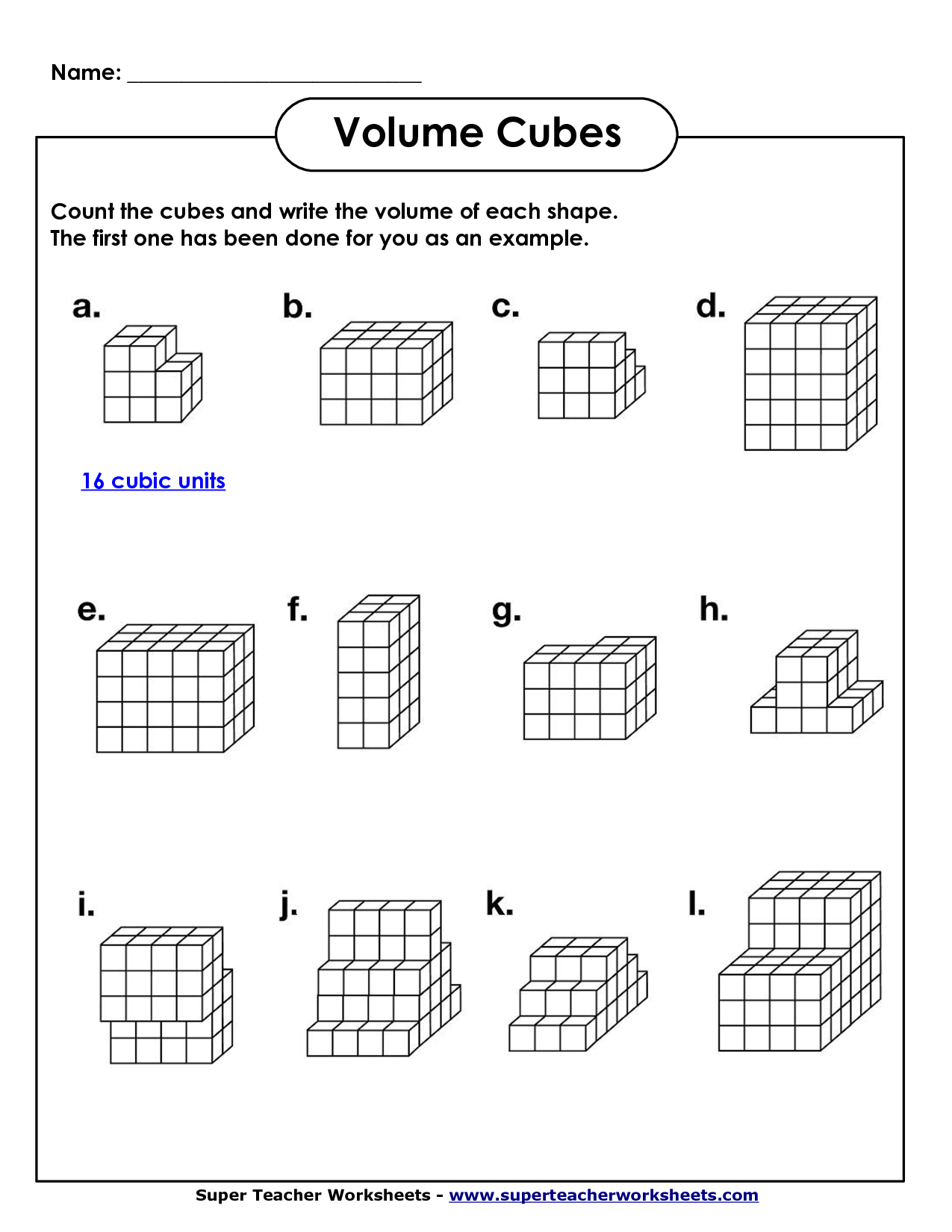
  Volume of a Rectangular Prism Worksheet 1 – Here

---

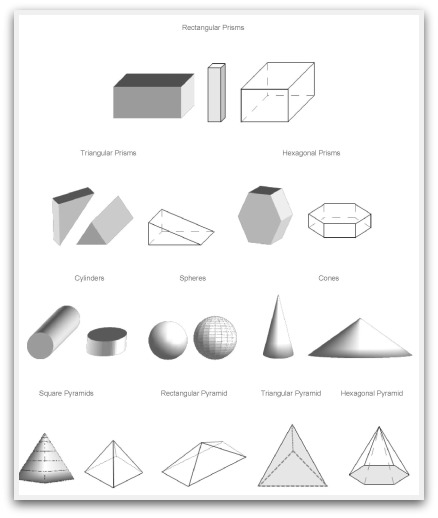
  3D Geometric Shapes

---

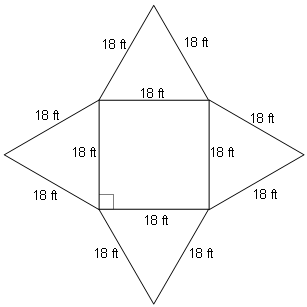
  Surface Area Square Pyramid Net

---

  Kindergarten Worksheets 3D Shapes Printables

---

  3D Shapes Worksheets

---

  Rectangular Prism Volume Worksheet

---

  Pentagonal Prism Net

---

  Round to Nearest Tenth Find the Area of the the Figure

---

  Three-Dimensional Shapes Cut Outs

---

  Compound Word Game

---

  Compound Word Game

---

What is a geometry net?

A geometry net is a 2-dimensional pattern that can be folded to create a 3-dimensional solid shape. It is essentially a blueprint that shows all the faces of a shape unfolded and laid flat, allowing for visualization and understanding of the shape's structure and dimensions.

What is the purpose of using geometry nets in mathematics?

The purpose of using geometry nets in mathematics is to help visualize and understand three-dimensional shapes in two dimensions. By unfolding a net of a 3D shape, students can see the relationships between its faces, edges, and vertices, as well as study its properties and calculate its surface area and volume more easily. This hands-on approach allows for a deeper understanding of geometry concepts and aids in problem-solving and spatial reasoning skills.

How are geometry nets used in creating three-dimensional shapes?

Geometry nets are two-dimensional representations of three-dimensional shapes that can be cut out and folded to create the shape. By visualizing the flat net as a map of how the shape fits together, it can help in understanding the structure of the three-dimensional object and how its faces are connected. When the net is folded along the crease lines, it forms the desired three-dimensional shape, making it a useful tool for visualization and construction in geometry.

Can any shape be represented using a geometry net?

Not every shape can be represented using a geometry net. A geometry net is a 2-dimensional representation of a 3-dimensional object, so shapes that are not fully enclosed or have intersecting parts cannot be accurately represented using a net. Additionally, some complex shapes may require multiple nets to be fully represented.

What are some common examples of geometry nets?

Some common examples of geometry nets include cubes, rectangular prisms, triangular prisms, pyramids, cylinders, cones, and spheres. These nets can be folded and assembled to create the respective 3D shapes. Each net shows the pattern that needs to be folded to form the shape and is a helpful tool for understanding the relationship between 2D shapes and their three-dimensional counterparts.

How can geometry nets help in visualizing three-dimensional shapes?

Geometry nets are two-dimensional representations that can be cut out and folded to create three-dimensional shapes. By using geometry nets, individuals can visualize the faces, edges, and vertices of a three-dimensional shape in a more tangible and interactive way. This hands-on approach allows for a better understanding of the spatial relationships within the shape, helping to reinforce concepts such as surface area and volume.

What are the key characteristics of a well-designed geometry net?

A well-designed geometry net should have all faces of the 3D object represented, accurately reflecting the shapes and sizes of each face. The net should be able to be folded to form the 3D shape without any overlaps or gaps. It should also have clear labeling or numbering of vertices, edges, and faces to aid in assembly, and should be easy to understand and manipulate for the intended purpose of visualizing the 3D shape.

Can you fold a geometry net to form different shapes?

Yes, a geometry net is a 2D shape that can be cut out and folded to create 3D shapes such as cubes, pyramids, prisms, and more. By following the crease lines and folding the net appropriately, you can transform it into various 3D shapes, providing a visual representation of geometric concepts.

How can geometry nets be used in problem-solving activities?

Geometry nets can be used in problem-solving activities by allowing students to visualize and manipulate 3D shapes in a 2D format, making it easier to analyze and understand the properties of the shape. By cutting out, folding, and assembling the nets, students can explore the relationships between faces, edges, and vertices of the shapes. This hands-on approach helps students develop spatial reasoning skills, problem-solving abilities, and a deeper understanding of geometric concepts. Additionally, nets can be used to investigate surface area, volume, and symmetry of various geometric shapes, providing a practical and engaging way to solve geometric problems.

How do geometry nets relate to the concepts of surface area and volume in mathematics?

Geometry nets are two-dimensional representations of three-dimensional shapes that can be folded to form the actual 3D shape. They help visualize the surface area and volume of complex 3D objects by showing how the faces of the shape fit together and how the object can be unfolded and laid flat. By analyzing the dimensions of the nets, it becomes easier to calculate the surface area of the faces and the volume of the enclosed shape since the nets provide a clear view of the dimensions and relationships between different parts of the object. Thus, geometry nets serve as a valuable tool in understanding and calculating surface areas and volumes in mathematics.