Geometric Transformations Worksheets

If you are searching for a reliable resource to enhance your knowledge and skills in geometric transformations, then look no further than our extensive collection of worksheets. Designed to cater to the needs of students and educators alike, our worksheets provide a comprehensive and structured approach to understanding the concepts and applications of geometric transformations. Whether you are a beginner or an advanced learner, our worksheets offer targeted exercises that focus on the core concepts and allow you to practice and refine your understanding of this important mathematical discipline.

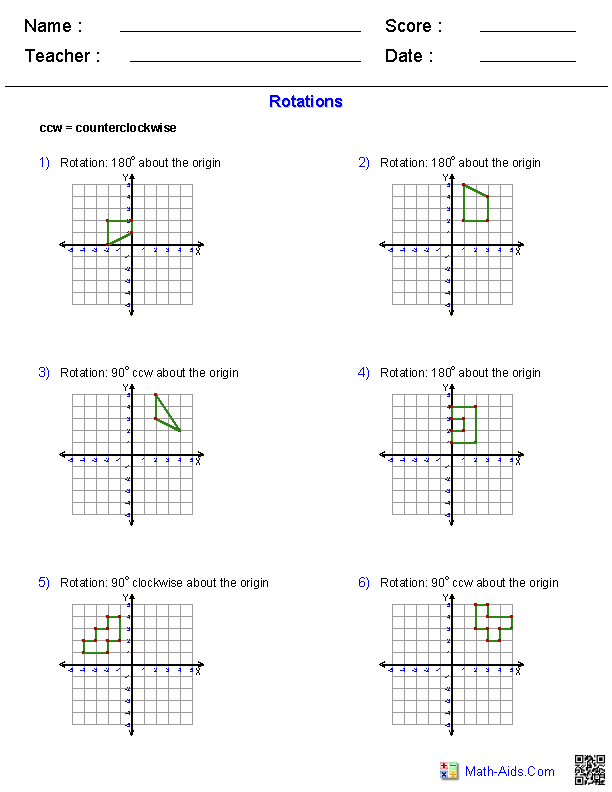
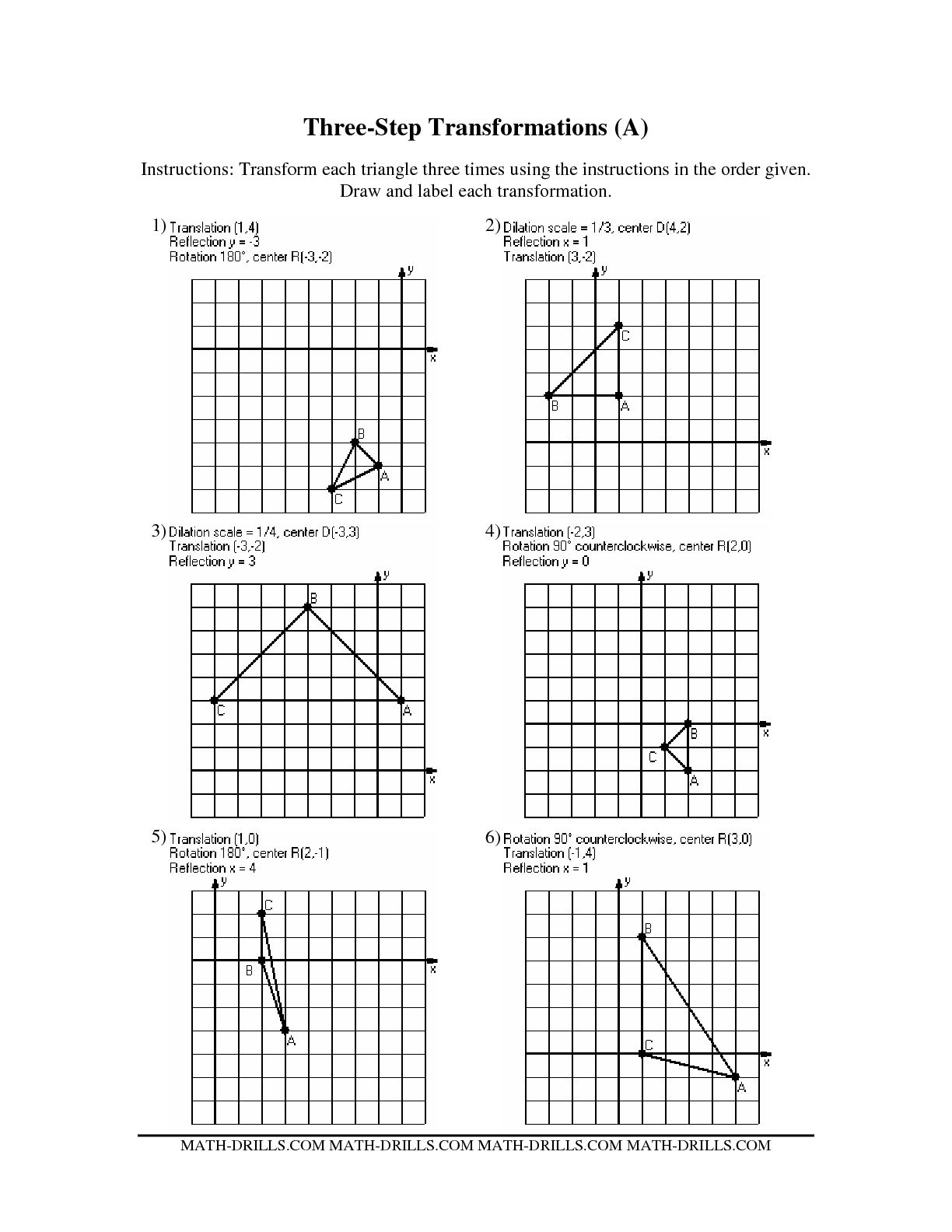
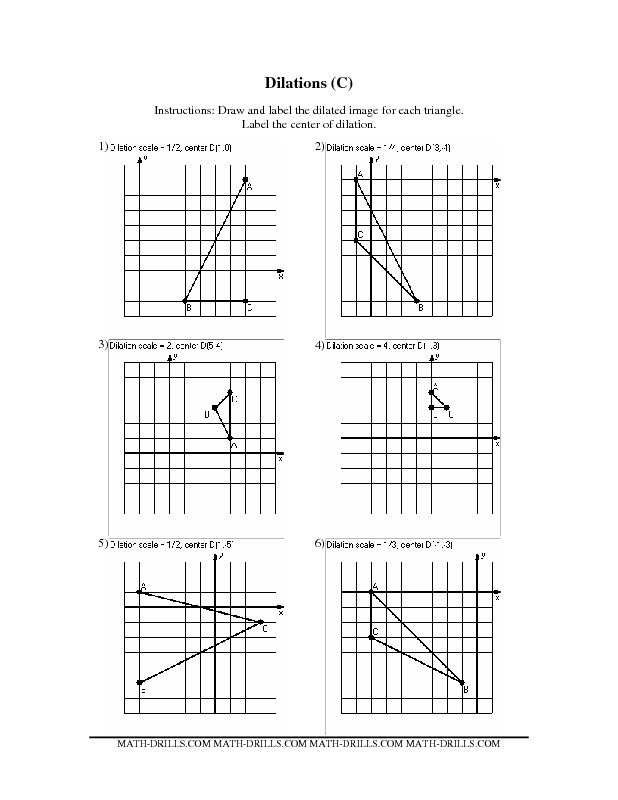
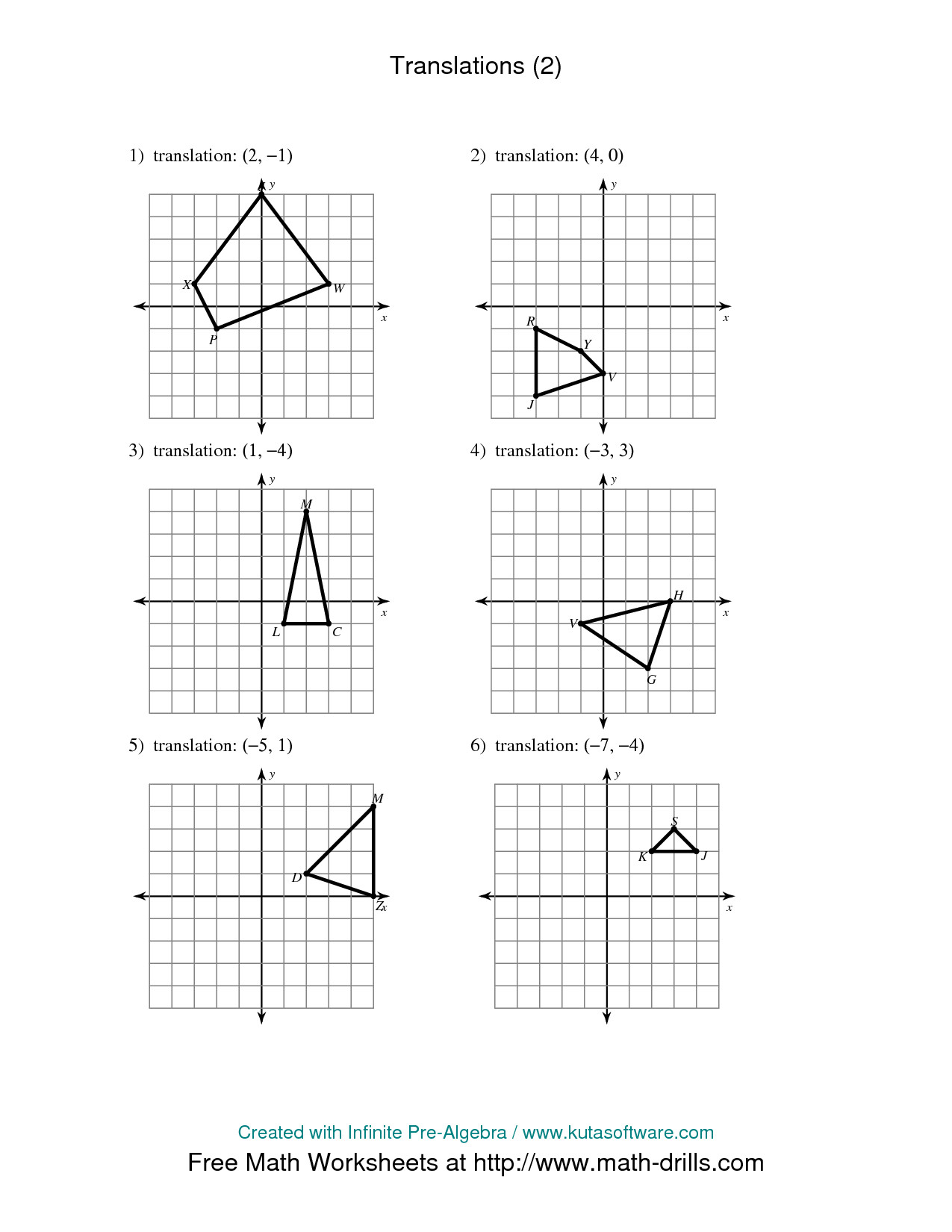
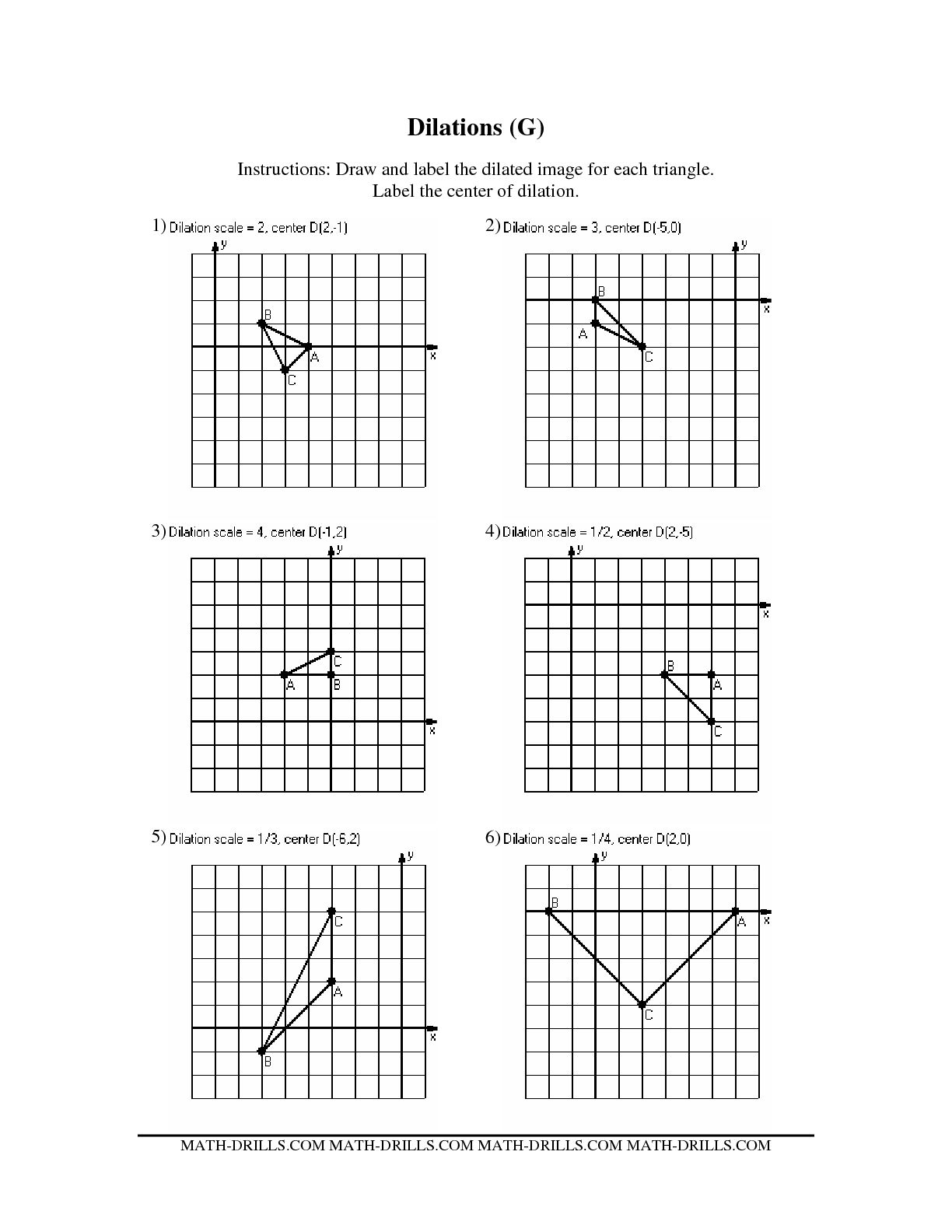
  Geometry Rotations Worksheet

---

  Transformations Math Worksheets

---

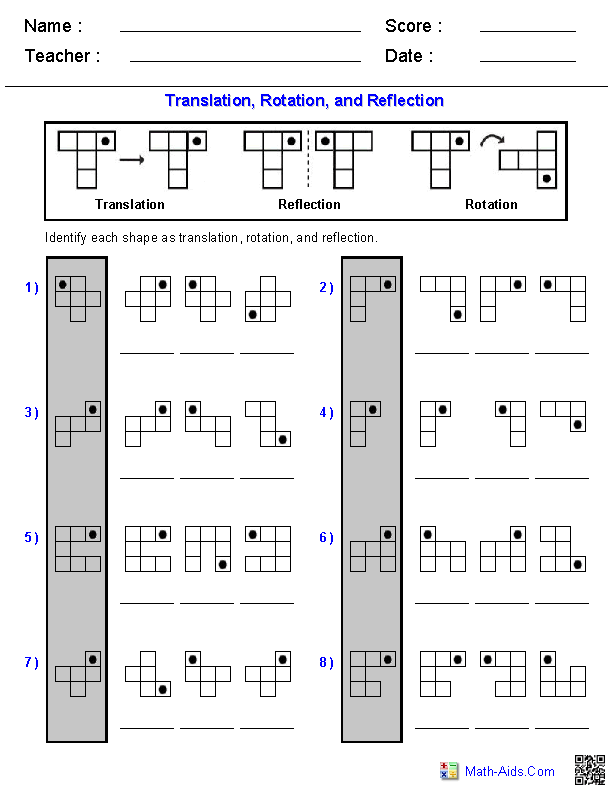
  Math Worksheets Reflection Rotation Translation

---

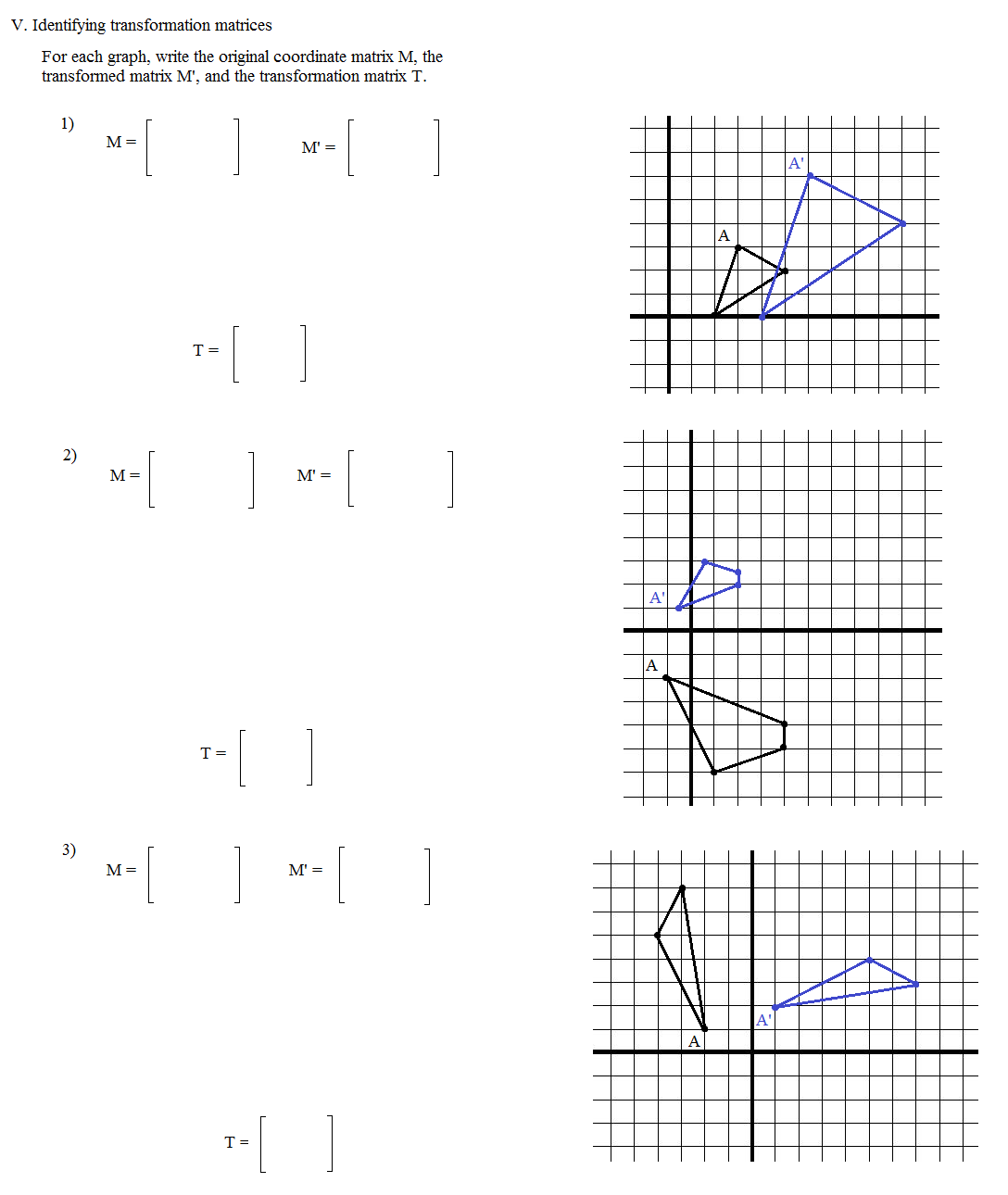
  Coordinate Geometry Worksheets

---

  Transformations Math Worksheets

---

  8th Grade Dilations Worksheet

---

  Translation Math Worksheets

---

  Transformation Worksheets Geometry

---

  Geometry Translation Reflection Rotation Worksheets

---

  Transformation Worksheets Geometry

---

What is a geometric transformation?

A geometric transformation refers to a change in the position, size, or shape of a geometric figure. This alteration can be achieved through translations (moving the figure to a different location), rotations (turning the figure around a fixed point), reflections (flipping the figure across a line), or dilations (changing the size of the figure while keeping its shape and proportions). Geometric transformations are fundamental concepts in mathematics and have applications in various fields such as computer graphics, engineering, and architecture.

What are the different types of geometric transformations?

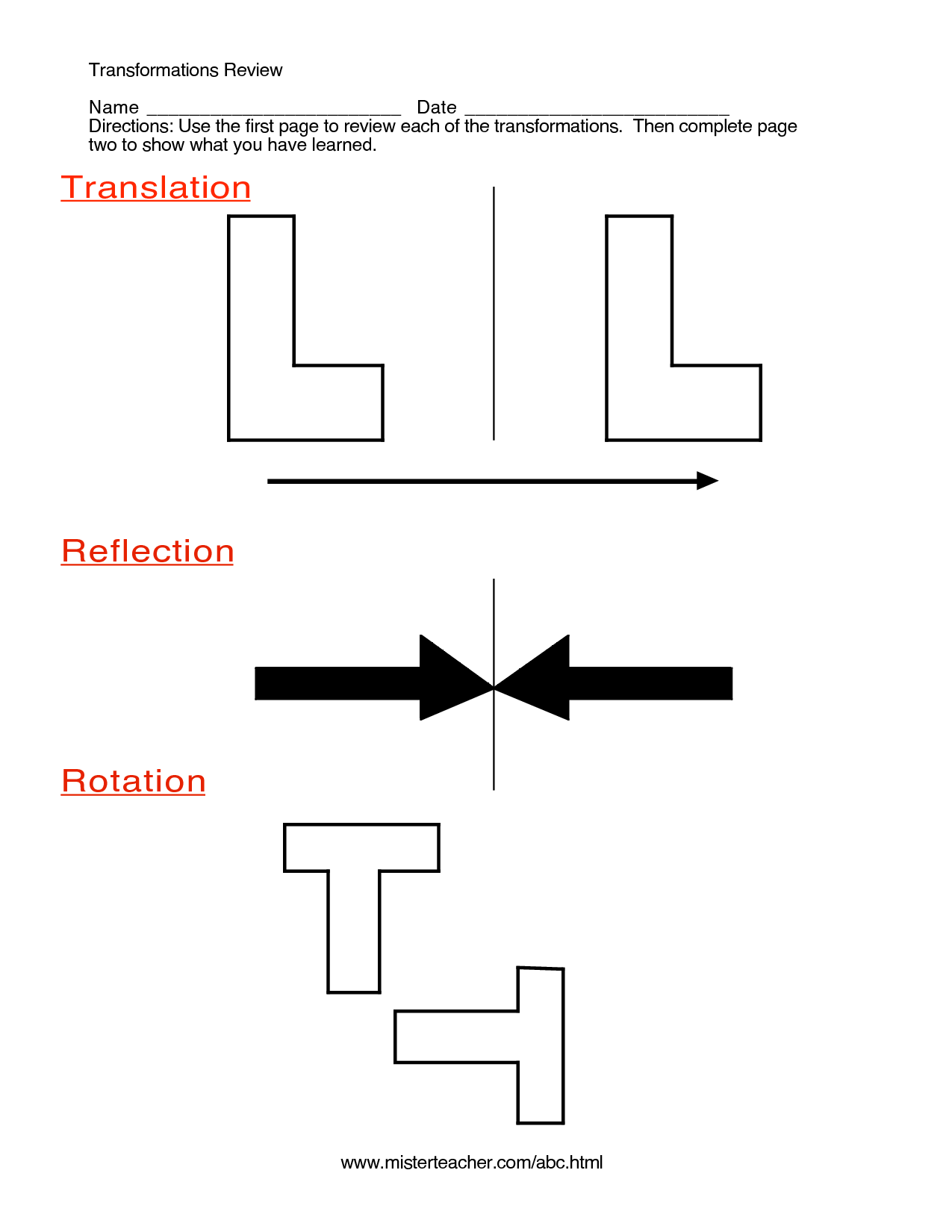
There are several types of geometric transformations, including translation (moving an object without rotating or resizing it), rotation (turning an object around a fixed point), reflection (flipping an object over a line), dilation (resizing an object proportionally), shear (slanting an object in a particular direction), and projection (mapping points in three-dimensional space onto a two-dimensional plane). Each of these transformations plays a crucial role in geometry and visual arts.

What are the properties of a translation transformation?

A translation transformation is a type of transformation that moves an object from one location to another without changing its size, shape, or orientation. The properties of a translation transformation include shifting the object horizontally and/or vertically, preserving the parallelism of lines and the distance between points, and being reversible and cumulative with other translations. Additionally, translations do not change the angles between lines or the orientation of the object being transformed.

How does a rotation transformation affect an object?

A rotation transformation changes the orientation of an object by turning it around a fixed point, known as the center of rotation. It does not change the shape or size of the object, but rather repositions it in a new orientation relative to its original position. The angle of rotation determines how much the object is turned, with a 90-degree rotation resulting in a quarter turn, a 180-degree rotation resulting in a half turn, and so on.

What is the difference between a reflection and a rotation transformation?

A reflection transformation involves flipping a shape across a line, such as a mirror image, while a rotation transformation involves turning a shape around a point by a certain degree. In other words, a reflection results in a mirror image of the original shape, whereas a rotation changes the orientation of the shape while keeping its size and proportions the same.

How does a dilation transformation change the size of an object?

A dilation transformation changes the size of an object by either enlarging or shrinking it while preserving its shape. If the dilation factor is greater than 1, the object will be enlarged, making it bigger. Conversely, if the dilation factor is between 0 and 1, the object will be shrunk, making it smaller. The distance between every point on the object and the center of dilation is multiplied by the dilation factor, resulting in a proportional increase or decrease in size of the object.

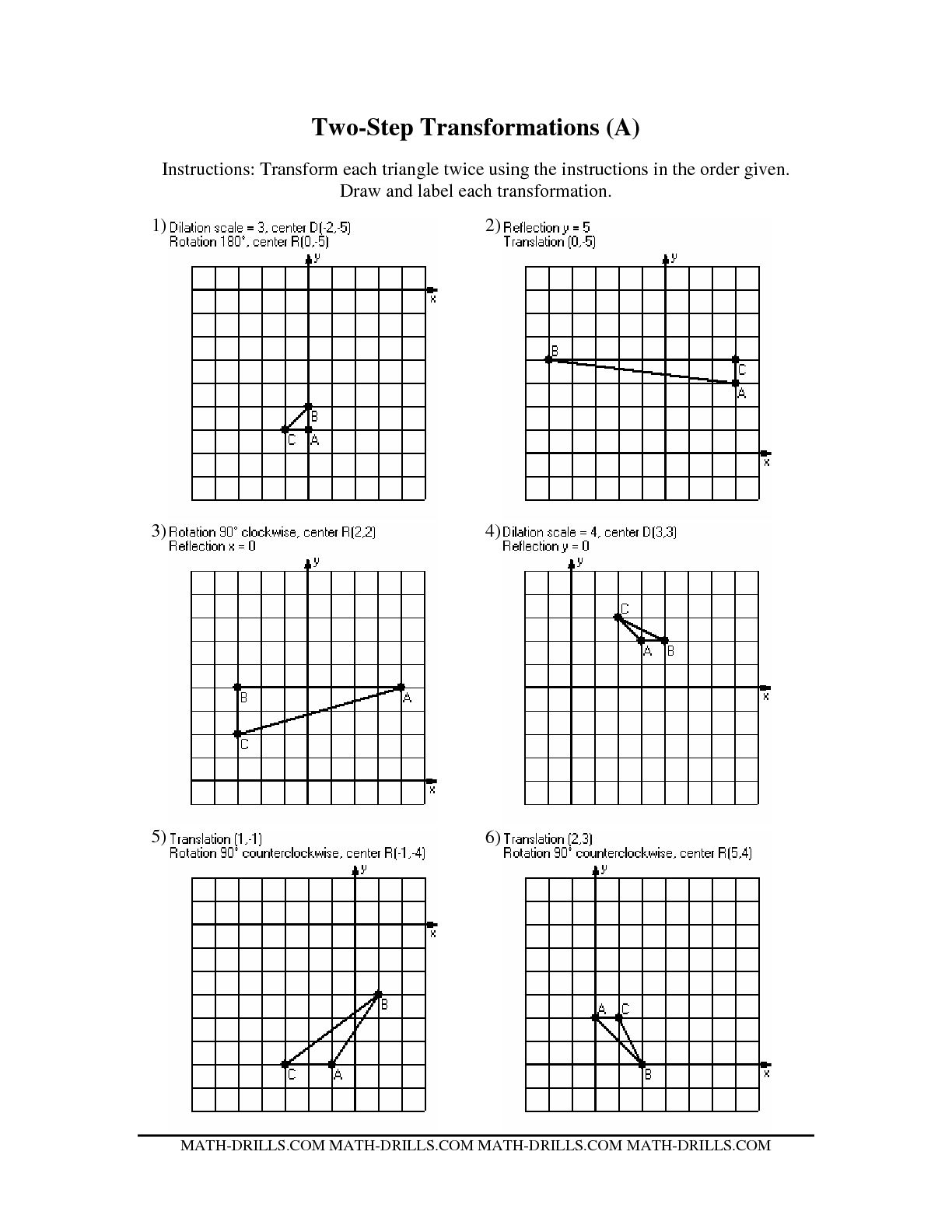
How are two or more geometric transformations combined?

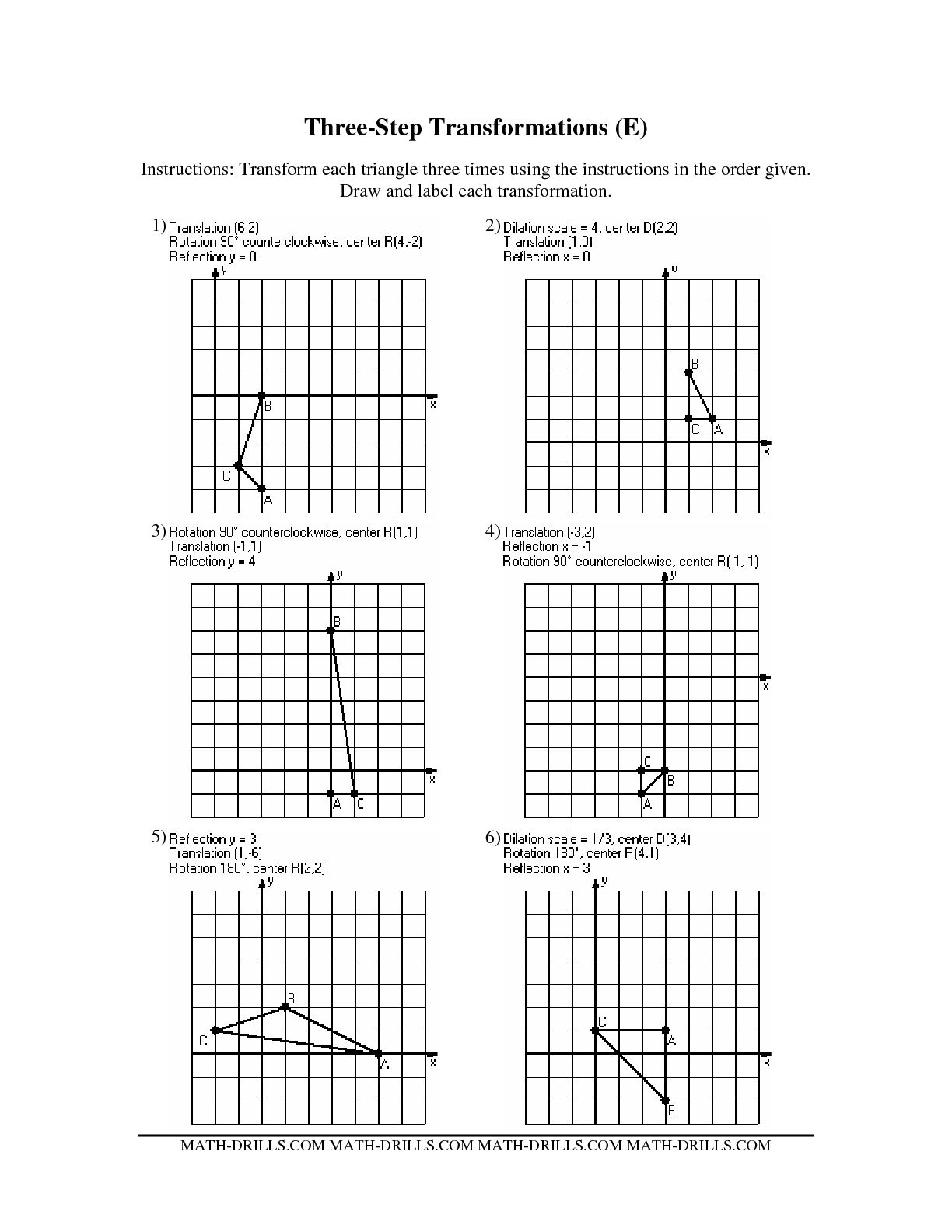
Two or more geometric transformations are combined by applying them sequentially, one after the other, in the order specified. This means that the output of the first transformation becomes the input for the next transformation. By chaining transformations together, you can create a new composite transformation that is equivalent to applying each individual transformation in succession.

What is the difference between a composition and a decomposition of transformations?

A composition of transformations involves applying two or more transformations in a specific order to achieve a single combined transformation, while a decomposition of transformations involves breaking down a single transformation into a sequence of simpler transformations. In essence, composition is about combining transformations to create a new single transformation, whereas decomposition is about breaking down a complex transformation into simpler components.

How does a tessellation relate to geometric transformations?

A tessellation is created by repeating a shape over and over again to completely cover a plane without any gaps or overlaps. Geometric transformations such as translation, rotation, reflection, and dilation can be applied to the original shape to create the tessellation. These transformations help in positioning and adjusting the shape in a way that it fits together seamlessly when repeated to form the pattern of the tessellation.

How are geometric transformations used in real-life applications?

Geometric transformations are used in a variety of real-life applications such as computer graphics (to create animations and special effects), image processing (to edit and enhance photos), engineering (to design structures and machinery), architecture (to plan and visualize buildings), and navigation systems (to map and locate routes). These transformations help in resizing, rotating, translating, and distorting objects to represent real-world scenarios and provide solutions for practical problems efficiently and accurately.