Free- Associative Property Math Worksheets
Are you searching for math worksheets that focus on the concept of associative property? Look no further! Our free Associative Property Math Worksheets are designed to help students understand and apply this important mathematical principle. Whether you are a teacher looking for engaging classroom resources or a parent seeking additional practice for your child, our worksheets are the perfect tool to reinforce understanding of the associative property in a fun and interactive way.
Table of Images 👆
- Associative Property Multiplication
- Math Properties Worksheets 7th Grade
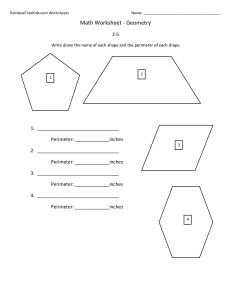
- Equation Worksheets
- Multiplicative Inverse Property Worksheet
- Linear Equations Examples and Answers
- 5th Grade Math Worksheets
- Foil Method Worksheets with Answers
- Foil Method Worksheets with Answers
- Foil Method Worksheets with Answers
- Foil Method Worksheets with Answers
- Foil Method Worksheets with Answers
- Foil Method Worksheets with Answers
- Foil Method Worksheets with Answers
More Math Worksheets
Printable Math WorksheetsMath Worksheets Printable
Printable Math Worksheets Multiplication
Math Worksheets for 2nd Graders
Math Practice Worksheet Grade 6
Math Multiplication Worksheets
First Grade Subtraction Math Worksheets Printable
Math Worksheets Integers
Superhero Math Worksheets
Middle School Math Coloring Worksheets
What is the free-associative property in math?
The free-associative property in math states that when adding or multiplying several numbers, the grouping of the numbers does not affect the result. In other words, you can regroup the numbers in any way you want and still get the same answer, which is especially helpful when working with long strings of numbers or terms.
How does the free-associative property affect addition?
The free-associative property states that when adding multiple numbers, the grouping of those numbers does not affect the result. This means that changing the order in which numbers are grouped and added together will not change the sum. For example, when adding three numbers like (2 + 3) + 4 or 2 + (3 + 4), the result will always be the same, which is 9 in this case. This property makes addition more flexible and easier to perform, as you can rearrange the numbers in any way without changing the final answer.
How does the free-associative property affect multiplication?
The free-associative property in multiplication means that you can change the grouping of numbers being multiplied without changing the result. This property allows you to rearrange the order in which multiplication is performed, making calculations more flexible and efficient. By rearranging the parentheses in a multiplication expression, you will get the same product, which can simplify complex calculations and allow for easier mental math strategies.
Can the free-associative property be applied to subtraction or division?
The free-associative property applies to addition and multiplication operations, but not to subtraction or division. This property allows changing the grouping of numbers without affecting the result, which is not possible with subtraction or division as changing the order of operands can lead to different outcomes.
How can the free-associative property help simplify calculations?
The free-associative property helps simplify calculations by allowing us to regroup or change the order of the numbers being operated on without changing the final result. This property applies to addition and multiplication, which means we can group numbers together in different ways and still arrive at the same answer. By taking advantage of this property, we can rearrange numbers in a way that makes calculations easier and more efficient, ultimately simplifying the process of solving mathematical problems.
Is the free-associative property limited to just two numbers or can it be applied to multiple numbers?
The free-associative property can be applied to multiple numbers, not just two numbers. This property states that when adding or multiplying a set of numbers together, the grouping of the numbers does not affect the result. In other words, you can group the numbers in any way you want and still get the same answer.
Can the free-associative property be used with variables or only with numbers?
The free-associative property can be used with both variables and numbers. This property states that for any set of numbers or variables, you can group them in any way you want when adding or multiplying them without changing the result. This means that the order in which you group the numbers or variables does not affect the final sum or product.
Are there any limitations or restrictions when applying the free-associative property?
One limitation of the free-associative property is that it may not be applicable in all mathematical operations or situations. It primarily works with addition and multiplication operations in algebraic expressions but may not hold true for other mathematical operations or under certain conditions. Additionally, applying free association requires keeping the order of terms intact, which may not always be possible or appropriate depending on the math problem at hand.
Can you provide an example of how the free-associative property is used in a math problem?
Sure! An example of the free-associative property in math is as follows: (2 + 3) + 4 = 2 + (3 + 4). This property shows that when adding three or more numbers together, the sum will be the same regardless of how the numbers are grouped.
How can understanding the free-associative property help solve more complex math equations?
Understanding the free-associative property in math allows individuals to simplify and manipulate complex equations by regrouping numbers or variables without changing the outcome. This can make solving equations more efficient and help identify patterns or relationships that might not be immediately obvious. By leveraging the free-associative property, mathematicians can streamline calculations and gain insights into the underlying structure of mathematical problems, ultimately making it easier to tackle more complex equations with confidence and accuracy.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.







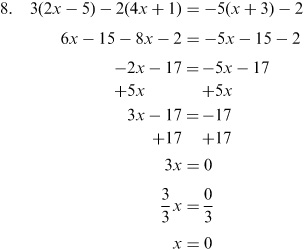


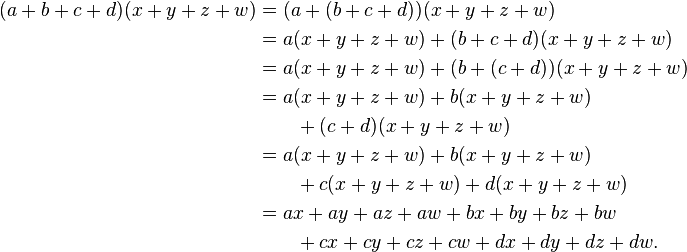

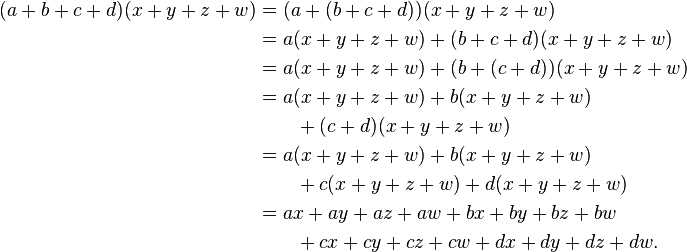
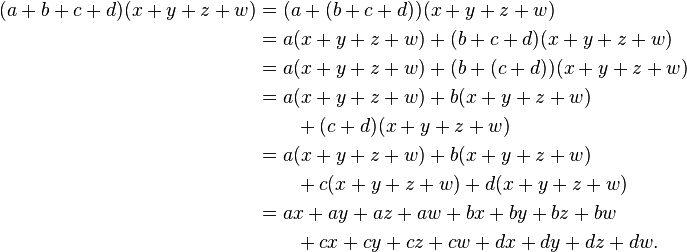
















Comments