Finding Volume of Prism Worksheets

Are you a middle school or high school student looking for worksheets that can help you practice finding the volume of prisms? Look no further! These worksheets are designed to provide you with plenty of practice problems that will strengthen your understanding of this important geometry concept. By focusing on the entity of prisms and their subject, volume, these worksheets will give you the opportunity to apply the formulas and concepts you have learned in class.

  Rectangular Prism Volume Worksheet

---

  Cubes Volume Irregular Shapes

---

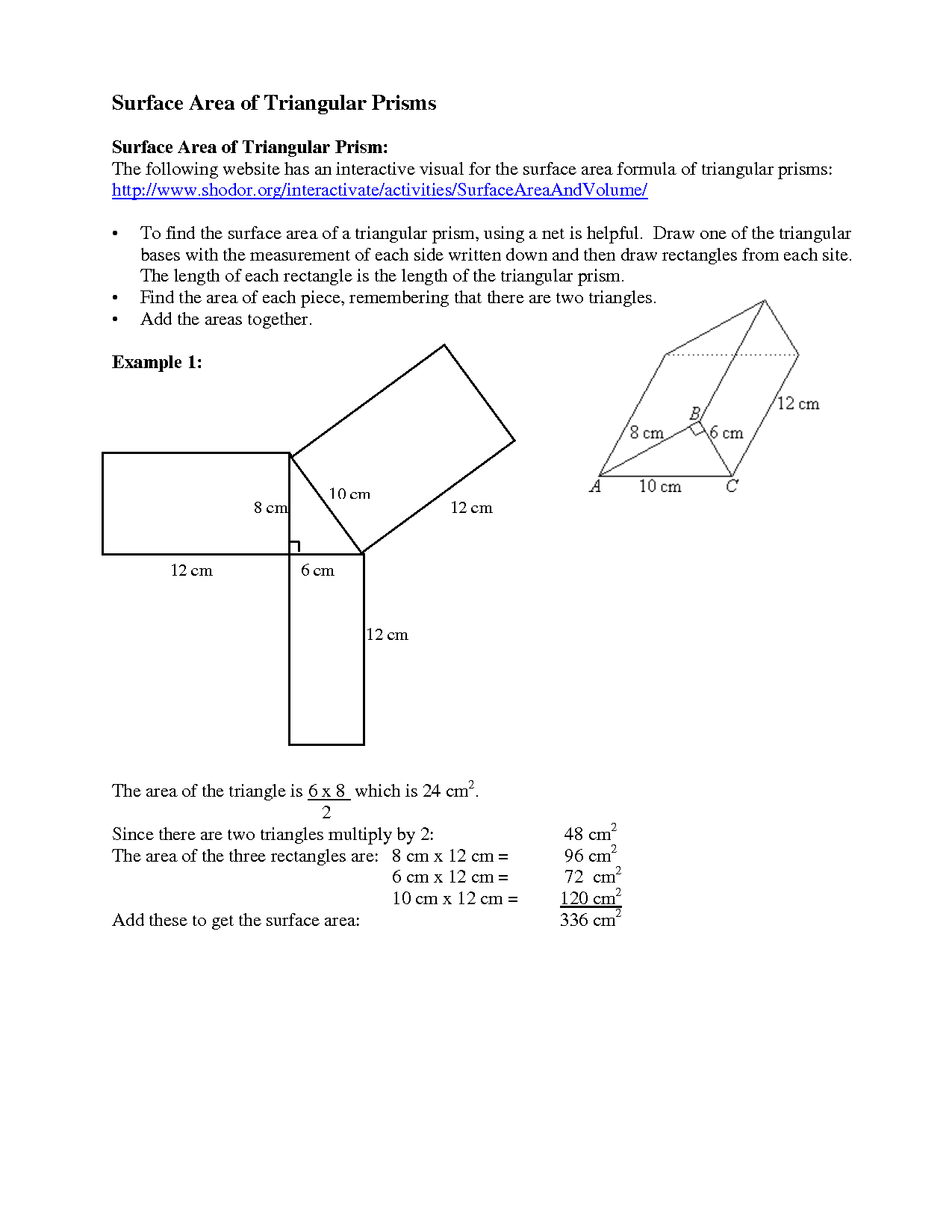
  Triangular Prism Surface Area Worksheet

---

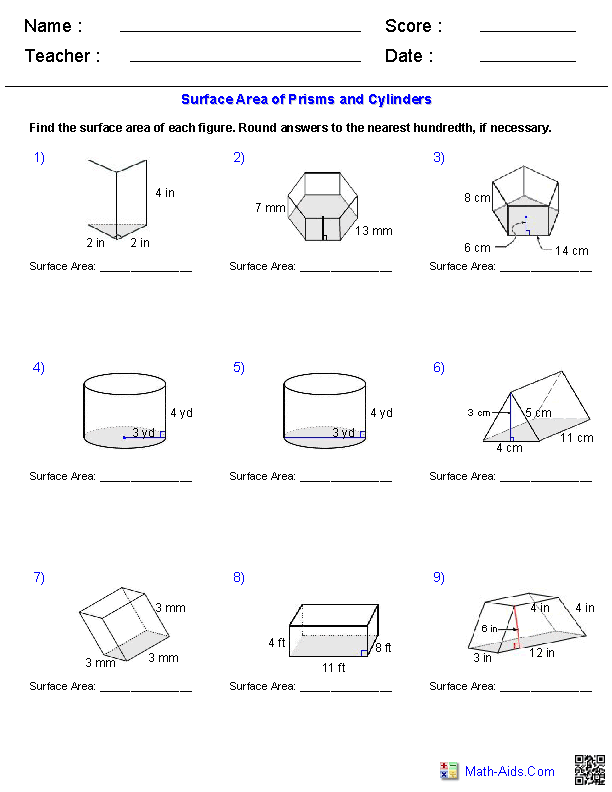
  Geometry Surface Area and Volume Worksheets

---

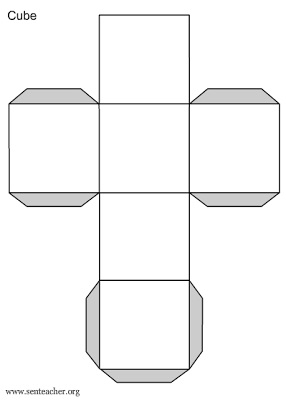
  3D Shape Nets to Print

---

  Space Measurement Units

---

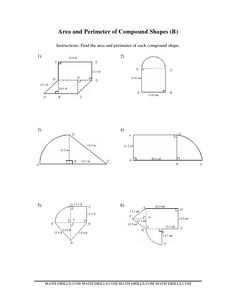
  Compound Area Worksheet

---

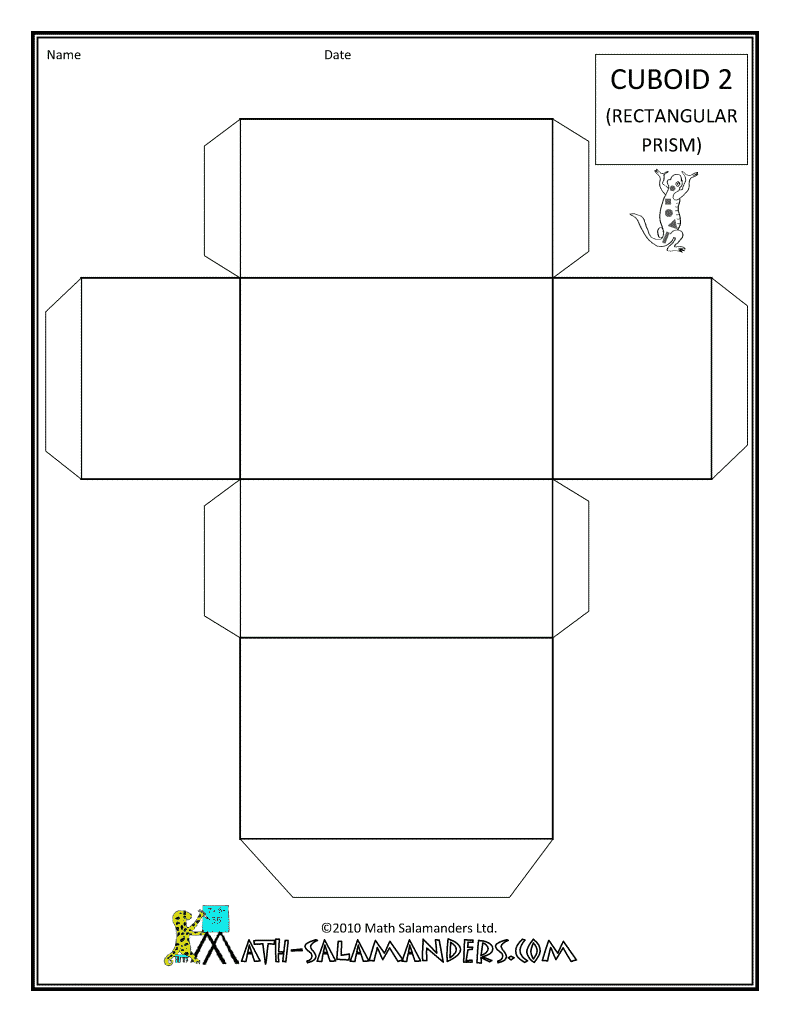
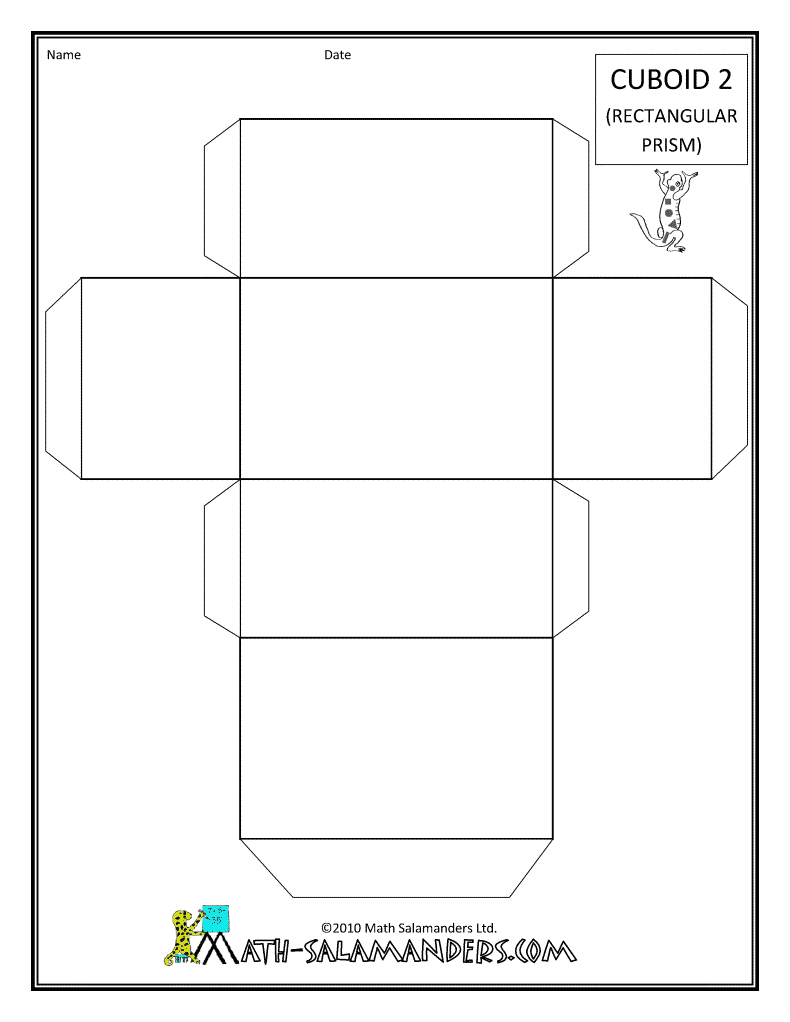
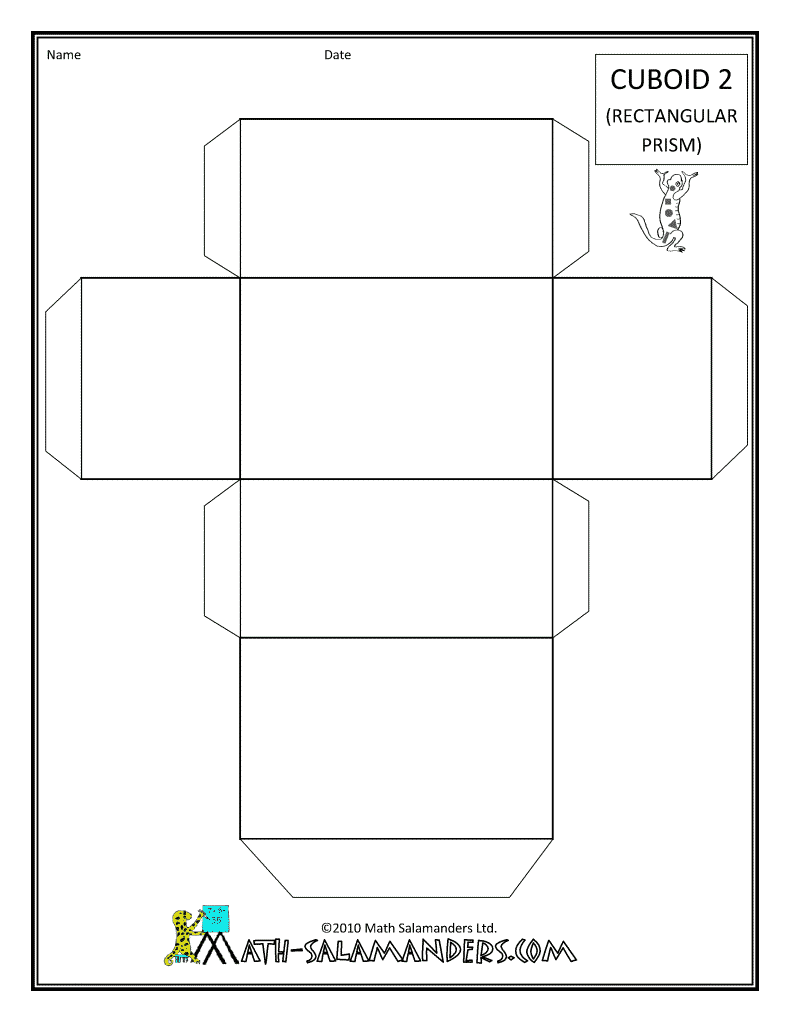
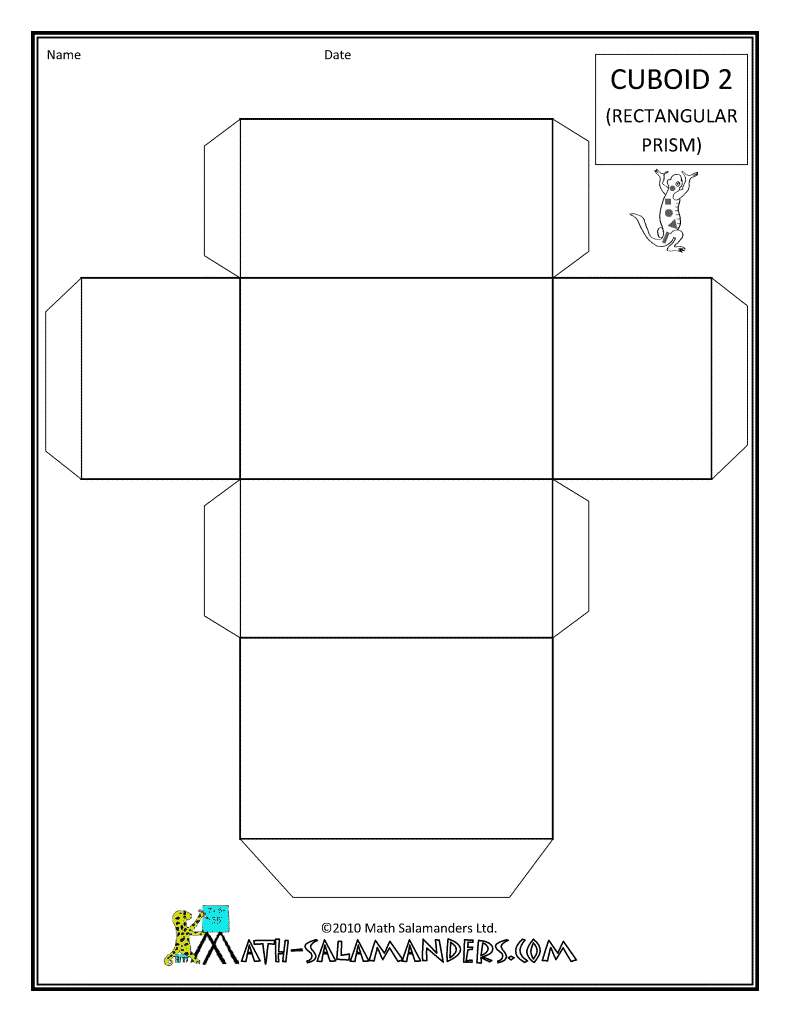
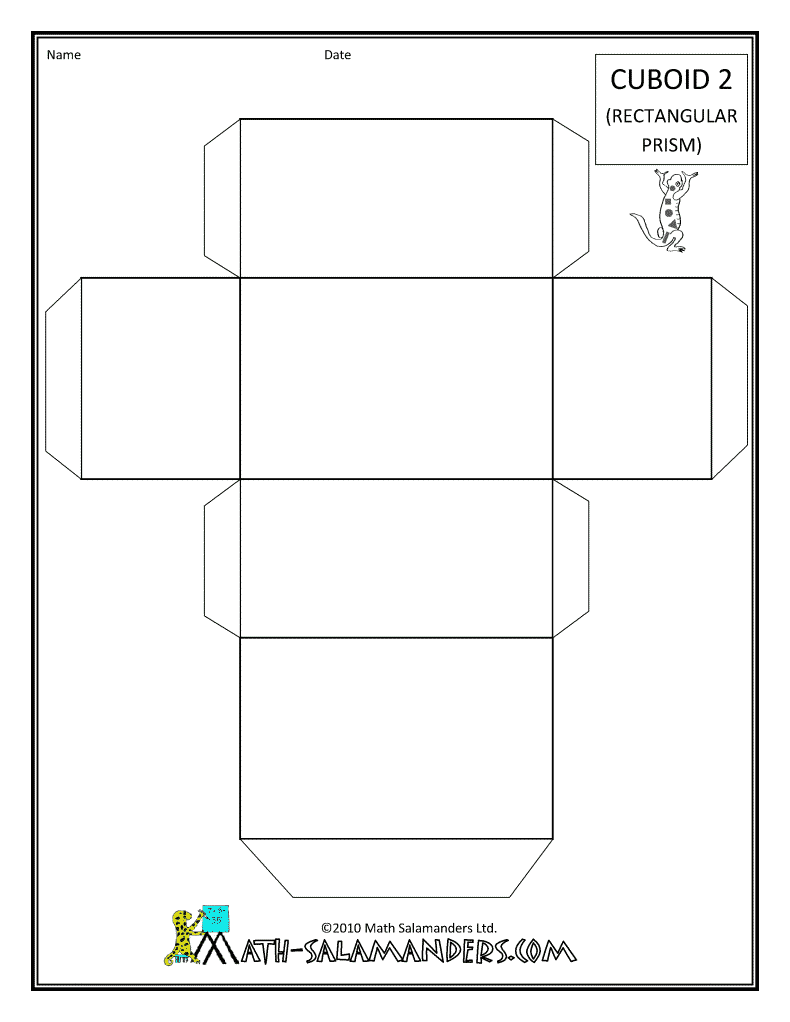
  Rectangular Prism Net

---

  Rectangular Prism Net

---

  Rectangular Prism Net

---

  Rectangular Prism Net

---

  Rectangular Prism Net

---

  Rectangular Prism Net

---

What is the formula for finding the volume of a prism?

The formula for finding the volume of a prism is V = Bh, where V represents the volume, B is the area of the base of the prism, and h is the height of the prism.

Name two different types of prisms.

Two different types of prisms are rectangular prisms, which have rectangular faces, and triangular prisms, which have triangular faces.

What are the dimensions needed to find the volume of a rectangular prism?

To find the volume of a rectangular prism, you need to know the length, width, and height of the prism. Multiply these three dimensions together (length x width x height) to calculate the volume of the rectangular prism.

How can you determine the height of a triangular prism when given a side length and area?

To determine the height of a triangular prism when given a side length and area, you can use the formula for the area of a triangular prism, which is Area = 1/2 * base * height, where the base is the side length provided. You can rearrange this formula to solve for height by dividing the area by 1/2 times the base. This will give you the height of the triangular prism.

What is the volume of a prism with a length of 8 cm, width of 5 cm, and height of 10 cm?

To calculate the volume of a prism, you multiply the length, width, and height. So, for the given prism with a length of 8 cm, width of 5 cm, and height of 10 cm, the volume would be 8 cm * 5 cm * 10 cm = 400 cubic centimeters.

How do you calculate the volume of a cylinder prism?

To calculate the volume of a cylinder prism, you use the formula V = Bh, where B represents the base area of the prism (which is the area of the circle at the base of the cylinder) and h represents the height of the cylinder. The formula for the base area of a cylinder is B = ?r^2, where r is the radius of the base circle. To find the volume of the cylinder prism, you multiply the base area (?r^2) by the height of the cylinder.

What is the volume of a triangular prism with a base length of 6 meters, base width of 4 meters, and height of 12 meters?

The volume of a triangular prism is determined by multiplying the area of its base by its height. Since the base of the prism is a triangle, the area of the base is calculated as 0.5 x base length x base width, which gives us 0.5 x 6 x 4 = 12 square meters. Therefore, multiplying this base area by the height of the prism (12 meters) gives us a volume of 144 cubic meters.

How does the volume of a prism change if the dimensions are doubled?

If the dimensions of a prism are doubled, the volume of the prism will increase by a factor of 8. This is because volume is calculated by multiplying the length, width, and height of the prism together, so doubling each dimension means that the volume will be 2 x 2 x 2 = 8 times larger than the original volume.

Compare and contrast the volume of a rectangular prism and a cube with the same dimensions.

The volume of a rectangular prism and a cube with the same dimensions is calculated using the formula V = l × w × h and V = s^3, respectively. While both shapes have three dimensions, the rectangular prism has different lengths for each side (length, width, and height), resulting in a variable volume depending on these measurements. On the other hand, a cube has all sides equal in length, making its volume a fixed value no matter the specific dimensions. Despite this difference, both shapes have a volume proportional to the product of their dimensions, but the cube's volume is more straightforward to calculate due to its symmetrical nature.

How does the volume of a prism compare to the volume of its base shape?

The volume of a prism is directly proportional to the volume of its base shape. In particular, the volume of a prism is equal to the area of its base shape multiplied by the height of the prism. Therefore, if the base shape of a prism is doubled in size, the volume of the prism will also be doubled. This relationship holds true for prisms of any shape or size.