Factoring Worksheet with a 1

Factoring is an essential skill that students need to master in algebra. It is a process of breaking down polynomial expressions into simpler forms. For students who are looking to practice and strengthen their knowledge of factoring, a factoring worksheet with a 1 as the greatest common factor provides a suitable solution.

  Factoring Polynomials Worksheet

---

  Factoring Trinomials Practice Worksheet

---

  Fun Factoring Quadratics Worksheet

---

  Algebra 2 Factoring Polynomials Worksheet with Answers

---

  Algebra 2 Factoring Puzzle Worksheet

---

  Multiplication of Exponents and Division Worksheets

---

  Kuta Software Infinite Algebra 1 Answers Key

---

  Simplifying Rational Expressions Worksheets

---

  Writing Linear Equations Worksheet Answer Key

---

  Finding the Value of X Algebra Worksheet

---

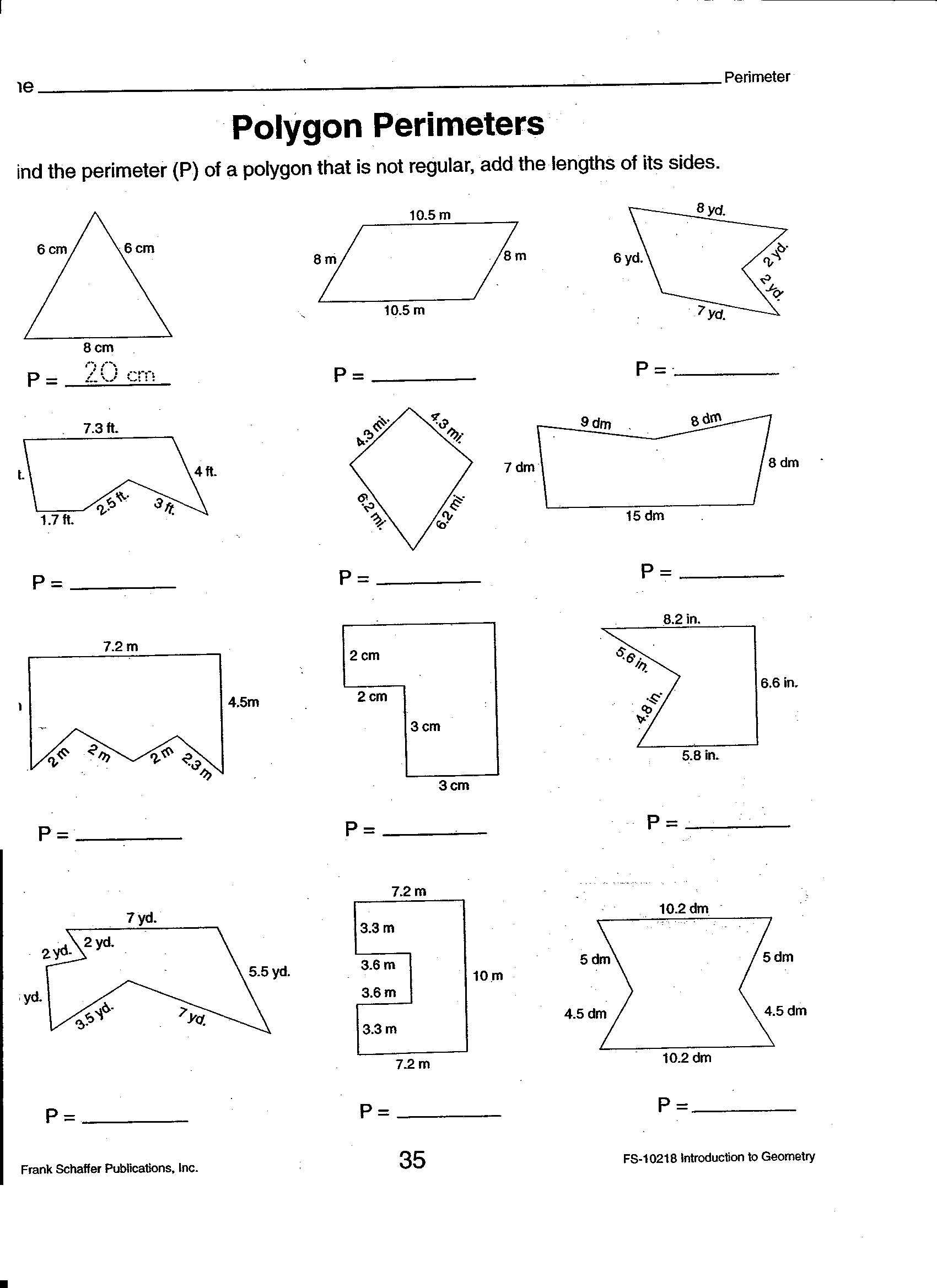
  Formula Area and Perimeter Worksheets

---

  Order of Operations Worksheets 6th Grade

---

  Factor Each Completely Assignment Algebra 2

---

  Translating Algebraic Expressions Worksheets

---

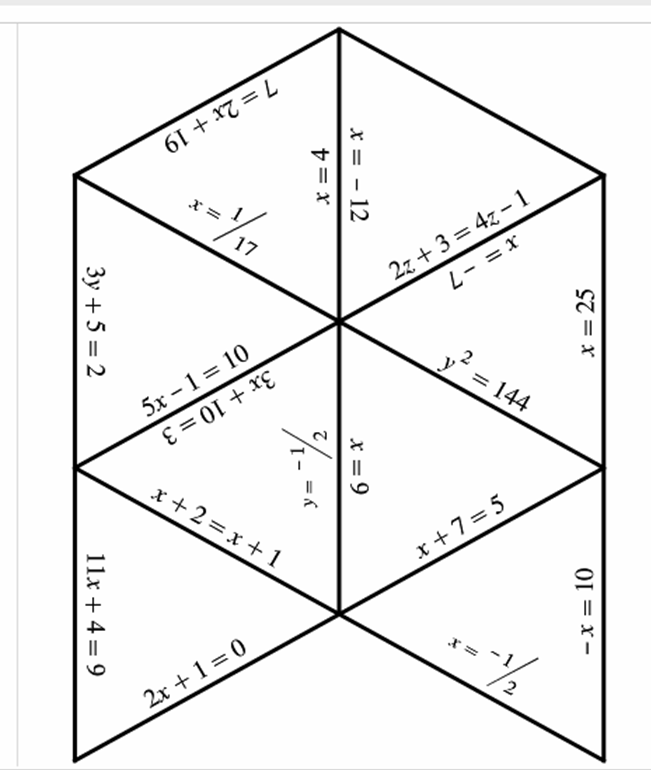
  Quadratic Equations Puzzle

---

What is factoring?

Factoring is the process of finding the factors of a given mathematical expression. This involves breaking down the expression into simpler components that can be multiplied together to produce the original expression. Factoring is commonly used in algebra to solve equations, simplify expressions, and identify patterns in mathematics.

Why is factoring important in mathematics?

Factoring is important in mathematics because it allows us to simplify and solve complex equations, as well as identify common factors. It is crucial for various mathematical operations, such as finding the roots of polynomials, analyzing number patterns, and simplifying fractions. Factoring plays a key role in algebra, number theory, and calculus, helping us understand relationships between different numbers and equations, and making problem-solving more efficient and systematic.

What is the difference between factoring and expanding?

Factoring is the process of breaking down an algebraic expression into simpler parts, often by finding common factors and writing it as a product of these factors. On the other hand, expanding involves simplifying an expression by multiplying out brackets and combining like terms to make it more detailed and explicit. In essence, factoring involves going from a complex expression to a simpler form, while expanding does the opposite by making an expression more complex.

How can factoring help in simplifying algebraic expressions?

Factoring can help in simplifying algebraic expressions by breaking down complex expressions into simpler forms. It involves finding common factors among different terms and grouping them together. This process can help to reveal patterns and simplify the expression by reducing the number of terms and simplifying calculations. Factoring also helps in identifying common factors that can be canceled out, leading to a more concise and manageable form of the expression.

What are the common methods used for factoring quadratic equations?

The common methods used for factoring quadratic equations are the factoring by grouping, factoring trinomials, difference of squares, and completing the square. Each method utilizes different algebraic techniques to break down the quadratic equation into its linear factors. These techniques are often applied based on the structure of the quadratic equation and the coefficients of the terms involved.

How can factoring be used to solve real-world problems?

Factoring can be utilized to solve real-world problems by breaking down complex expressions or equations into simpler components, leading to a better understanding of the relationship between variables and facilitating the identification of solutions. In scenarios involving finance, engineering, or sciences, factoring can help in analyzing data, making predictions, optimizing processes, and solving equations more efficiently, ultimately aiding decision-making and problem-solving in various real-world contexts.

How does factoring relate to finding the roots of an equation?

Factoring involves breaking down an equation into its individual factors, which can help in identifying the roots or solutions of the equation. When an equation is factored, it becomes easier to see where the equation equals zero, as each factor represents a potential root. By identifying the factors of an equation and setting each factor equal to zero, you can determine the values that make the equation true and thereby find the roots of the equation. This relationship between factoring and finding roots is particularly useful in algebra and solving polynomial equations.

Can factoring be used to simplify fractions?

Yes, factoring can be used to simplify fractions. By factoring the numerator and denominator of a fraction and canceling out common factors, the fraction can be simplified to its lowest terms. This process helps to reduce the size of the numbers involved and make the fraction easier to work with or interpret.

What are some common mistakes to avoid when factoring expressions?

Some common mistakes to avoid when factoring expressions include not properly identifying the greatest common factor, incorrectly applying the distributive property, forgetting to check for a difference of squares or perfect square trinomial, and overlooking potential opportunities to simplify before factoring. Additionally, rushing through the factoring process without double-checking your work or not fully understanding the rules and techniques for factoring can lead to errors. It's essential to take your time, pay attention to detail, and practice regularly to improve your factoring skills and avoid these common mistakes.

How can factoring be applied in finding the greatest common factor (GCF) of several numbers?

Factoring can be applied in finding the greatest common factor (GCF) of several numbers by identifying the prime factors of each number and determining the common factors among them. Once the prime factors are found, the GCF can be obtained by multiplying the common prime factors with the lowest exponent they appear in across all numbers. This method simplifies the process of determining the GCF by breaking down the numbers into their basic factors and identifying the highest common factor among them.