Factoring Binomials Worksheet with Answers

A factoring binomials worksheet with answers is a helpful tool for students who are studying algebra and want to practice their skills in factoring expressions. This worksheet provides a range of problems with binomial expressions that need to be factored, and comes with step-by-step solutions to help students understand the process. With this worksheet, students can enhance their understanding of factoring and improve their problem-solving abilities in algebra.

  Factoring Polynomials Worksheet

---

  Algebra 1 Factoring Polynomials Worksheet with Answers

---

  Algebra 2 Factoring Worksheets with Answers

---

  Factoring Polynomials Worksheet with Answers

---

  Factoring Binomials Worksheet

---

  Factoring Trinomials Worksheet Answer Key

---

  Polynomials and Factoring Practice Worksheet Answers

---

  Greatest Common Factor Worksheet Answers

---

  Factoring Trinomials Practice Worksheet

---

  Multiplying and Factoring Polynomials Worksheet

---

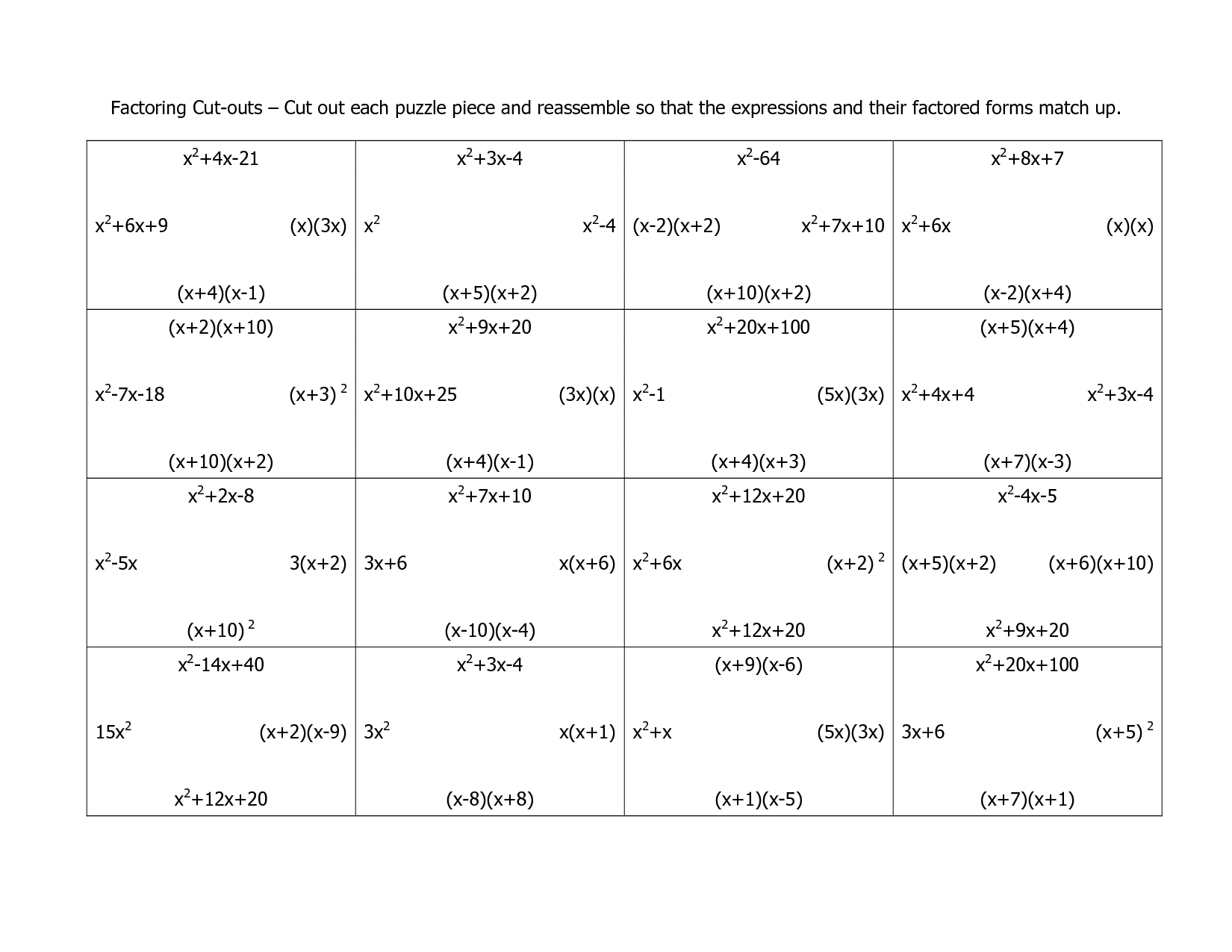
  Factoring Cut Out Puzzle Answers

---

  Factoring Trinomials Worksheet Coloring

---

  Factoring Polynomials Worksheet

---

  Algebra Factoring Polynomials Worksheet

---

  Algebra 2 Factoring Polynomials Worksheet 1

---

  Factoring Cubic Polynomials

---

  Factoring Trinomials Worksheets with Answers

---

  Algebra 2 Factoring Review Worksheet Answers

---

What is factoring?

Factoring is the process of breaking down a number into its smaller factors, which are whole numbers that can be multiplied together to give the original number. It is a fundamental concept in mathematics and is often used in algebra and number theory to simplify expressions, solve equations, and find common factors of numbers.

What are binomials?

Binomials are algebraic expressions containing two terms connected by either addition or subtraction. They are commonly written in the form of \(ax + by\), where \(a\) and \(b\) are coefficients, and \(x\) and \(y\) are variables. Binomials play a fundamental role in algebra and are frequently encountered in various mathematical expressions and equations.

How do you factor a binomial with a common factor?

To factor a binomial with a common factor, you simply factor out the common factor from both terms. This involves finding the greatest common factor (GCF) of the terms in the binomial and then dividing each term by this GCF. The result will be the factored form of the binomial with the common factor factored out.

How do you factor a binomial with a difference of squares?

To factor a binomial with a difference of squares, you need to identify that it is in the form of \(a^2 - b^2\). This expression can be factored into \((a + b)(a - b)\), where \(a\) and \(b\) are the square roots of the terms in the binomial. Simply apply this formula by replacing \(a\) and \(b\) with the square roots of the terms in the binomial to factor it correctly.

How do you factor a binomial with a perfect square trinomial?

To factor a binomial with a perfect square trinomial, you can simply take the square root of the first and last terms of the trinomial to get the binomial factors. In other words, if you have a perfect square trinomial in the form of (a + b)^2, then the factors of this trinomial will be (a + b).

How do you factor a binomial with a leading coefficient?

To factor a binomial with a leading coefficient, first identify if the leading coefficient is a common factor to both terms. If it is, factor it out. Then, look for common factors in the remaining terms and factor them out as well. Finally, see if the binomial can be factored further using techniques such as the difference of squares or sum/difference of cubes. It is important to practice factoring different types of binomials to become more proficient in this skill.

How do you factor a binomial with a non-leading coefficient?

To factor a binomial with a non-leading coefficient, first look for a common factor of the two terms. If there is one, factor it out. Then, use the AC method to factor the remaining trinomial by finding two numbers that multiply to the product of the leading coefficient and constant term, and add up to the coefficient of the linear term. Finally, rewrite the trinomial as a product of two binomials using the numbers found in the previous step.

How do you factor a binomial with a GCF and two different terms?

To factor a binomial with a greatest common factor (GCF) and two different terms, first factor out the GCF from both terms. Then, factor the remaining terms inside the parentheses using methods like grouping, difference of squares, or perfect squares. Finally, combine the factored GCF with the factored terms inside the parentheses to get the fully factored form of the binomial.

How do you factor a binomial with a quadratic trinomial?

To factor a binomial with a quadratic trinomial, you would need to look for common factors and apply the distributive property. First, check if there is a common factor in both terms. Then, determine if the trinomial is a perfect square trinomial or if it can be factored using techniques such as grouping, the difference of squares, or other factoring methods. Finally, write the factored form of the trinomial as a product of two binomials. Remember to double check your factoring by multiplying the binomials back out to confirm they equal the original trinomial.

How do you factor a binomial with a cubic trinomial?

To factor a binomial with a cubic trinomial, you can use the sum or difference of cubes formula: (a ± b)³ = a³ ± 3a²b + 3ab² ± b³. This formula helps you factorize the binomial into a trinomial. Simply substitute the terms in the formula and expand to get the factored form of the cubic trinomial.