Factor Polynomials by Grouping Worksheet
If you're a student or a teacher teaching algebra or polynomial factoring, you know the importance of having high-quality worksheets to help reinforce the concepts learned in class. And when it comes to worksheets that focus specifically on factoring polynomials by grouping, finding the right resource can make all the difference in the world.
Table of Images 👆
- Algebra 2 Factoring Polynomials Worksheet 1
- Factoring Polynomials Worksheet
- Factoring by Grouping Worksheet
- Algebra 2 Factoring Polynomials Worksheet 1
- Algebra 1 Factoring Polynomials Worksheet with Answers
- Factoring Polynomials Worksheet with Answers
- Polynomials and Factoring Practice Worksheet Answers
- Factoring Polynomials by Grouping Worksheets
- Algebra 2 Factoring Review Worksheet Answers
- Factoring Cubic Polynomials
- Algebra 2 Factoring Worksheets with Answers
- Factoring Polynomials by Grouping Worksheets
- Factor by Grouping
- Factoring by Grouping Examples
- Factoring Trinomials Worksheet
- Remainder and Factor Theorems
- Factoring by Grouping Worksheet Answers
- Factoring Polynomials by Grouping Problems
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Rosa Parks Worksheet Grade 1
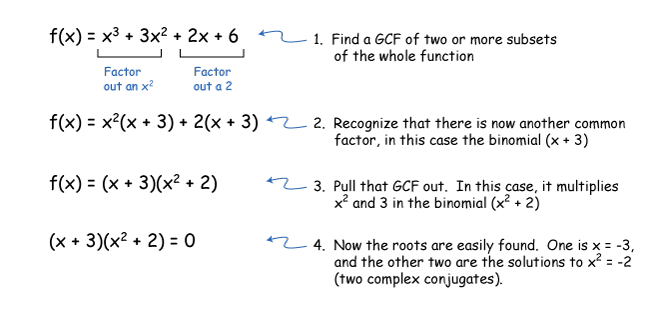
What is the purpose of factoring polynomials by grouping?
The purpose of factoring polynomials by grouping is to simplify complex polynomial expressions by grouping terms together in a way that makes it easier to factor out common factors. This method can help to organize the terms in a polynomial expression in a systematic manner, making the factoring process more straightforward and allowing for easier identification of common factors within the expression. Ultimately, factoring polynomials by grouping helps to break down a polynomial expression into simpler, more manageable factors, making it easier to work with and solve.
How do you identify if a polynomial can be factored by grouping?
To determine if a polynomial can be factored by grouping, check if the polynomial has an even number of terms and if the terms can be grouped in pairs with a common factor. Next, check if each pair of terms shares a common factor beyond just a constant. If both these conditions are met, the polynomial can likely be factored by grouping. Apply the method of grouping by factoring out the common factors from each group and then factor out the common binomial factor that remains from the grouped pairs.
What is the first step in factoring polynomials by grouping?
The first step in factoring polynomials by grouping is to group the terms in the polynomial into pairs, typically by looking for common factors or patterns that can help simplify the expression before factoring.
What should you look for when grouping terms in a polynomial?
When grouping terms in a polynomial, you should look for common factors or patterns among the terms that can be combined. Grouping can help simplify the expression by allowing you to factor out common terms or recognize patterns such as squares of binomials or differences of squares. By identifying these groupings, you can frequently simplify and factor the polynomial more easily.
How do you factor out a common factor when grouping terms?
To factor out a common factor when grouping terms, first identify the terms that share a common factor. Next, factor out this common factor by dividing each term by it. Finally, rewrite the expression using the factored out common factor and the remaining terms inside parentheses. This process helps simplify expressions by reducing them into more manageable and simplified forms.
What is the next step after grouping terms in a polynomial?
After grouping terms in a polynomial, the next step is to factor out the common terms from each group. This involves finding the greatest common factor (GCF) of each group and factoring it out to simplify the expression further. By factoring out the GCF, you can often make the polynomial easier to work with and may also reveal patterns or relationships that can help you solve the problem more efficiently.
How do you factor out the common binomial factor?
To factor out the common binomial factor from an expression, you need to identify the binomial term that is common to all terms in the expression. Once identified, you can pull out this common binomial factor by dividing each term of the expression by the binomial factor. This process simplifies the expression and allows you to rewrite it in factored form with the common binomial factor outside of parentheses and the remaining factors inside parentheses.
What should you do with the remaining terms after factoring out the common binomial factor?
After factoring out the common binomial factor, you should then look at the remaining terms to see if they can be further factored or simplified. Try to manipulate the remaining terms using different factoring techniques such as grouping, difference of squares, or special products to see if you can continue simplifying the expression. If the remaining terms cannot be factored further, then you have successfully factored out the common binomial factor.
How do you check if the factored expression is correct?
To check if a factored expression is correct, you can expand it back to its original form using the distributive property. Multiply out the factors to see if it simplifies back to the original expression. If it does, then your factoring is correct. If not, then there may be an error in the factoring process.
Can you apply the process of factoring by grouping to any polynomial?
Yes, factoring by grouping can be applied to any polynomial, as long as the polynomial has four or more terms. The process involves grouping terms together in pairs, factoring out the greatest common factor from each pair, and then factoring out a common binomial factor from the grouped terms. This method is effective in simplifying and factoring polynomials with multiple terms.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.
















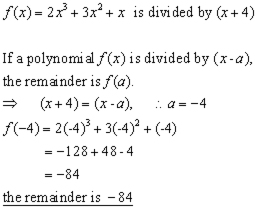

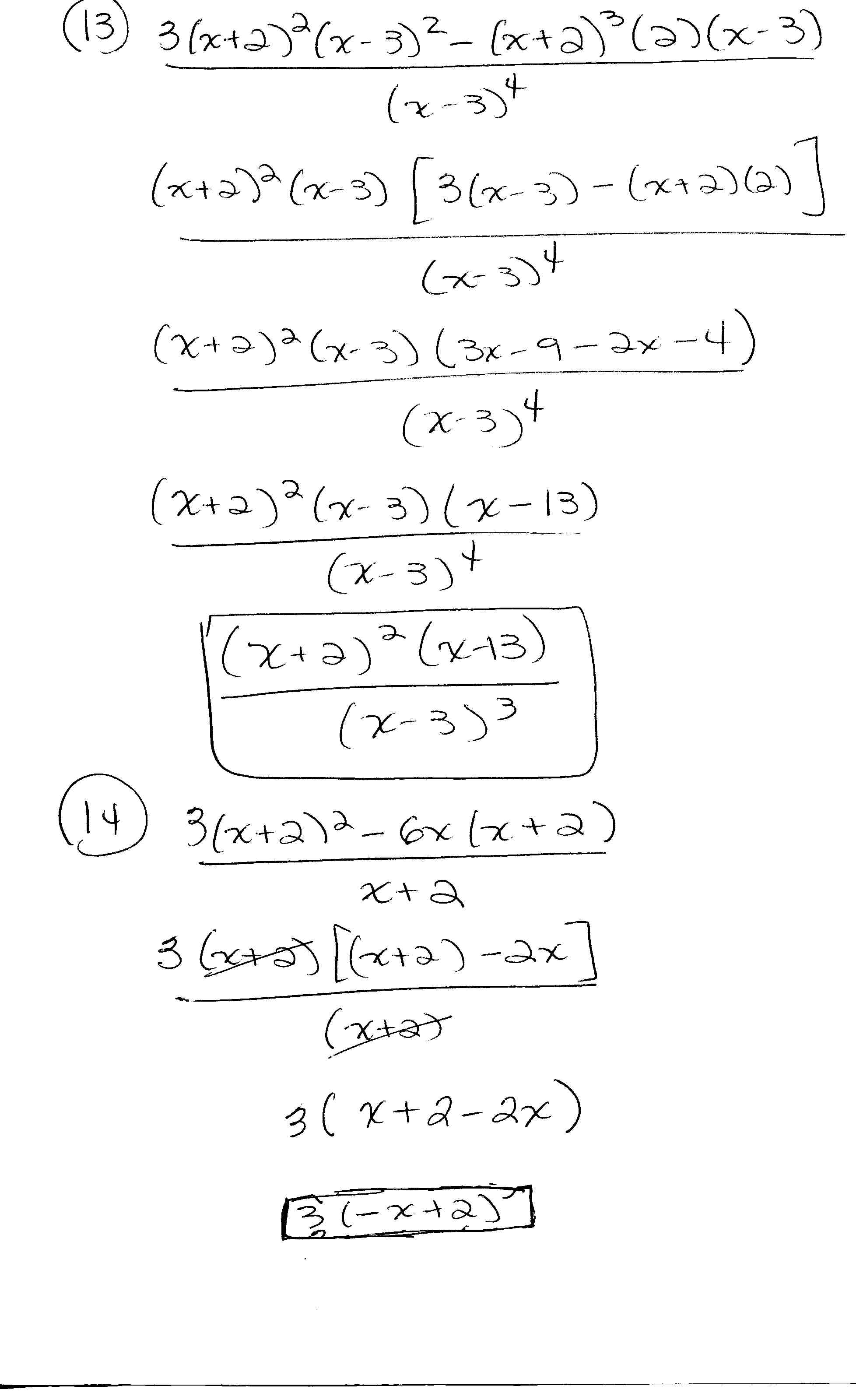














Comments