Factor and Prime Factorization Tree Worksheet

Are you searching for a comprehensive and engaging resource to help students understand factorization and prime factorization? This factor and prime factorization tree worksheet is designed to provide a structured approach for learners to explore and practice these mathematical concepts. With clear instructions and a variety of examples, this worksheet is perfect for students seeking to strengthen their understanding of factors and prime factors.

  Prime Factor Tree Worksheets

---

  Prime Factor Tree Worksheets

---

  Prime Factorization Chart

---

  Greatest Common Factor Venn Diagram

---

  7th Grade Math Worksheets

---

  Factors and Multiples Worksheets

---

What is a factor?

A factor is a number that can be evenly divided into another number. In other words, a factor is a divisor of a given number that, when multiplied together with other factors, equals that number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, as they can all divide evenly into 12 without leaving a remainder.

What is prime factorization?

Prime factorization is the process of finding a list of prime numbers that, when multiplied together, equal a given number. This is a fundamental concept in number theory where a composite number is broken down into its prime factors to understand its mathematical properties and relationships with other numbers.

How do you find the factors of a given number?

To find the factors of a given number, you can start by dividing the number by progressively larger integers starting from 1 and noting when the division results in no remainder. The divisors that divide the number without a remainder are the factors of the given number. Another approach is to find pairs of numbers that multiply together to give the original number, as these pairs are also factors of the number.

How is prime factorization related to finding factors?

Prime factorization is essential in finding factors of a number because it breaks down a number into its prime factors, which are the fundamental building blocks of the number. By listing out the prime factors of a number and their corresponding powers, we can easily determine all the factors of the original number by combining different combinations of these prime factors. This method simplifies the process of finding factors by providing a systematic approach based on the prime factorization of the number.

What is the difference between a prime number and a composite number?

A prime number is a whole number greater than 1 that can only be divided evenly by 1 and itself, whereas a composite number is a whole number greater than 1 that has more than two factors, meaning it can be divided evenly by at least one other number besides 1 and itself.

How can you determine if a number is prime or composite?

To determine if a number is prime or composite, you can check if it has any factors other than 1 and itself. If the number only has 1 and itself as factors, then it is prime. If it has other factors, then it is composite. One way to check for factors is to divide the number by all numbers up to its square root and see if any of them divide evenly. Alternatively, you can use more advanced methods like the Sieve of Eratosthenes or trial division.

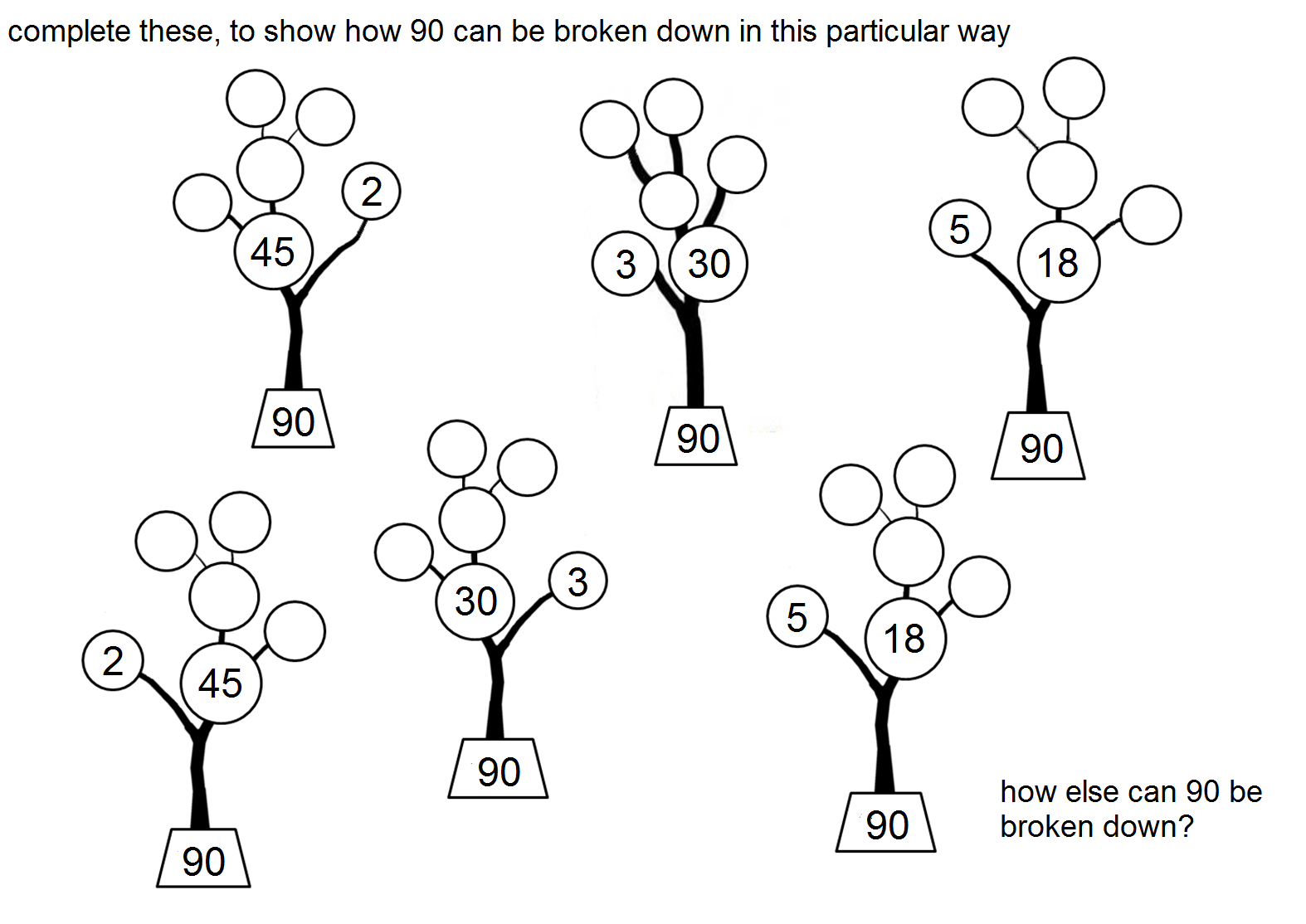
What is a factor tree and how is it used for prime factorization?

A factor tree is a visual tool used in mathematics to break a number down into its prime factors. It starts with the number at the top, and then branches out to display its factors, which are further factored into prime factors until all branches end in prime numbers. By using a factor tree, one can easily identify the prime factors of a number by continuously breaking down its factors until only prime numbers remain at the end of each branch, thus facilitating the process of prime factorization.

Can every number be represented as a product of its prime factors?

Yes, every positive integer greater than 1 can be represented as a product of its prime factors through a process known as prime factorization. This unique representation helps break down a number into a multiplication of its prime factors, which are the building blocks of numbers. This fundamental theorem of arithmetic is a key concept in number theory and mathematics.

Can prime factorization be used to simplify fractions?

Yes, prime factorization can be used to simplify fractions. By breaking down the numerator and denominator into their prime factors, you can identify common factors that can be cancelled out to simplify the fraction. This technique is particularly useful when dealing with large numbers or complex fractions, as it helps to reduce the fraction to its simplest form efficiently.

How can prime factorization be used in real-life situations?

Prime factorization is used in real-life situations such as cryptography for encoding and decoding messages securely, in computer algorithms for optimizing operations and solving complex problems efficiently, in the field of biology for studying genetic inheritance patterns, and in economics for analyzing market trends and predicting future behaviors. Additionally, prime factorization is used in engineering for designing efficient systems and in physics for understanding the structure of matter and energy. By breaking numbers down into their prime factors, we can gain insight and make connections across various disciplines and applications.