Exponent Worksheets with Integers

If you're a middle or high school student studying exponents and need extra practice with integers, we've got you covered. Our collection of exponent worksheets focuses specifically on the use of integers in exponent operations, providing you with ample opportunities to strengthen your understanding of this important mathematical concept. Whether you're just starting to learn about exponents or looking for a way to sharpen your skills, our worksheets offer a range of problems that will challenge and improve your knowledge.

  Negative Numbers Worksheets

---

  Order of Operations with Fractions Worksheets

---

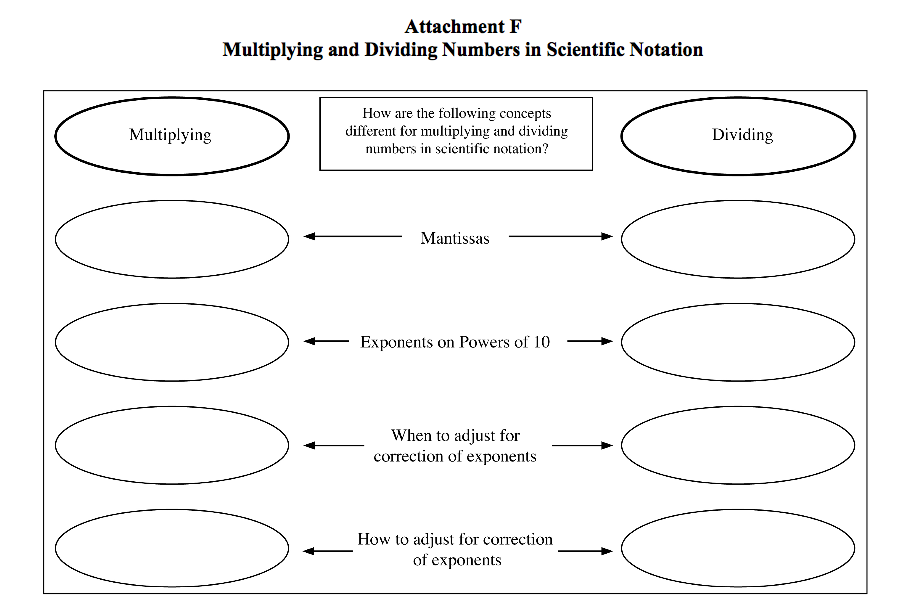
  Scientific Notation Graphic Organizer

---

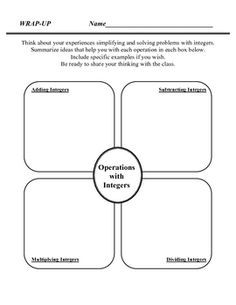
  Integer Rules Graphic Organizer

---

  Exponent Properties Worksheet

---

  Algebra 1 Radicals Worksheet

---

  1 Step Word Problems Worksheets

---

  One Hundred Chart Worksheet

---

  Multiplying Exponents

---

  Multiplying Exponents

---

  Multiplying Exponents

---

  Multiplying Exponents

---

  Multiplying Exponents

---

  Multiplying Exponents

---

  Multiplying Exponents

---

  Multiplying Exponents

---

What is an exponent?

An exponent is a superscript number that indicates how many times a number or expression should be multiplied by itself. It represents the power to which a number is raised. For example, in the expression 5^3, 5 is the base number and 3 is the exponent, indicating that 5 should be multiplied by itself three times.

How do you read an exponent expression?

To read an exponent expression, start by stating the base number, followed by the word "raised to the power of," and then the exponent which indicates how many times the base number is multiplied by itself. For example, "2 raised to the power of 5" indicates that 2 is multiplied by itself 5 times.

What is the base of an exponent expression?

The base of an exponent expression is the number that is being raised to a power. It is the value that is multiplied by itself a certain number of times as indicated by the exponent.

How do you calculate a positive exponent?

To calculate a positive exponent, you raise the base number to the power of the exponent. For example, to calculate 2^3, you would multiply 2 by itself three times, which equals 8 (2 * 2 * 2 = 8). So, in general, a^b is calculated by multiplying 'a' by itself 'b' times.

How do you calculate a negative exponent?

To calculate a negative exponent, you can rewrite it as the reciprocal of the base raised to the positive exponent. For example, if you have x^-3, you can calculate it by taking 1/x^3. Simply flip the base and change the negative exponent to a positive one to find the result.

What is the result when a number is raised to the power of 0?

When a number is raised to the power of 0, the result is always 1.

How do you simplify exponent expressions with the same base and different exponents?

To simplify exponent expressions with the same base and different exponents, you multiply the base and add the exponents. For example, if you have x^3 * x^5, you would add the exponents to get x^(3+5) = x^8. This rule works for any base raised to different exponents, simplifying the expression by combining like terms in this way.

How do you simplify exponent expressions with different bases and the same exponent?

To simplify exponent expressions with different bases and the same exponent, you can apply the property of exponents that states when you have the same exponent for different bases multiplied or divided, you can evaluate each base raised to the common exponent separately. For example, if you have 2^3 * 3^3, you can simplify this to (2 * 2 * 2) * (3 * 3 * 3) = 8 * 27 = 216. For division, like 4^2 / 2^2, you can simplify this to (4 / 2)^2 = 2^2 = 4.

What is the rule for multiplying exponential expressions with the same base?

When multiplying exponential expressions with the same base, you add the exponents while keeping the base the same. The rule can be stated as: a^m * a^n = a^(m+n), where 'a' is the common base and 'm' and 'n' are the exponents of the expressions being multiplied.

What is the rule for dividing exponential expressions with the same base?

When dividing exponential expressions with the same base, you subtract the exponents. For example, when dividing x^m by x^n (where x is the base), the result is x^(m-n). This rule applies when the bases of the exponential expressions are the same, and you are dividing them.