Evaluating Functions Worksheet Algebra 1
This blog post is designed to provide algebra 1 students with a helpful resource for evaluating functions. Understanding how to evaluate functions is a crucial skill in algebra, and these worksheets offer a range of practice problems to reinforce this concept. Whether you're a student looking to review or a teacher in need of additional materials, these worksheets are an excellent resource to strengthen your understanding of evaluating functions.
Table of Images 👆
- Exponents
- Algebra 1 Worksheets
- Evaluating Algebraic Expressions Worksheets
- Inverse Functions Algebra 1 Worksheet
- Free Printable Algebra 1 Worksheets
- Function Notation Worksheet
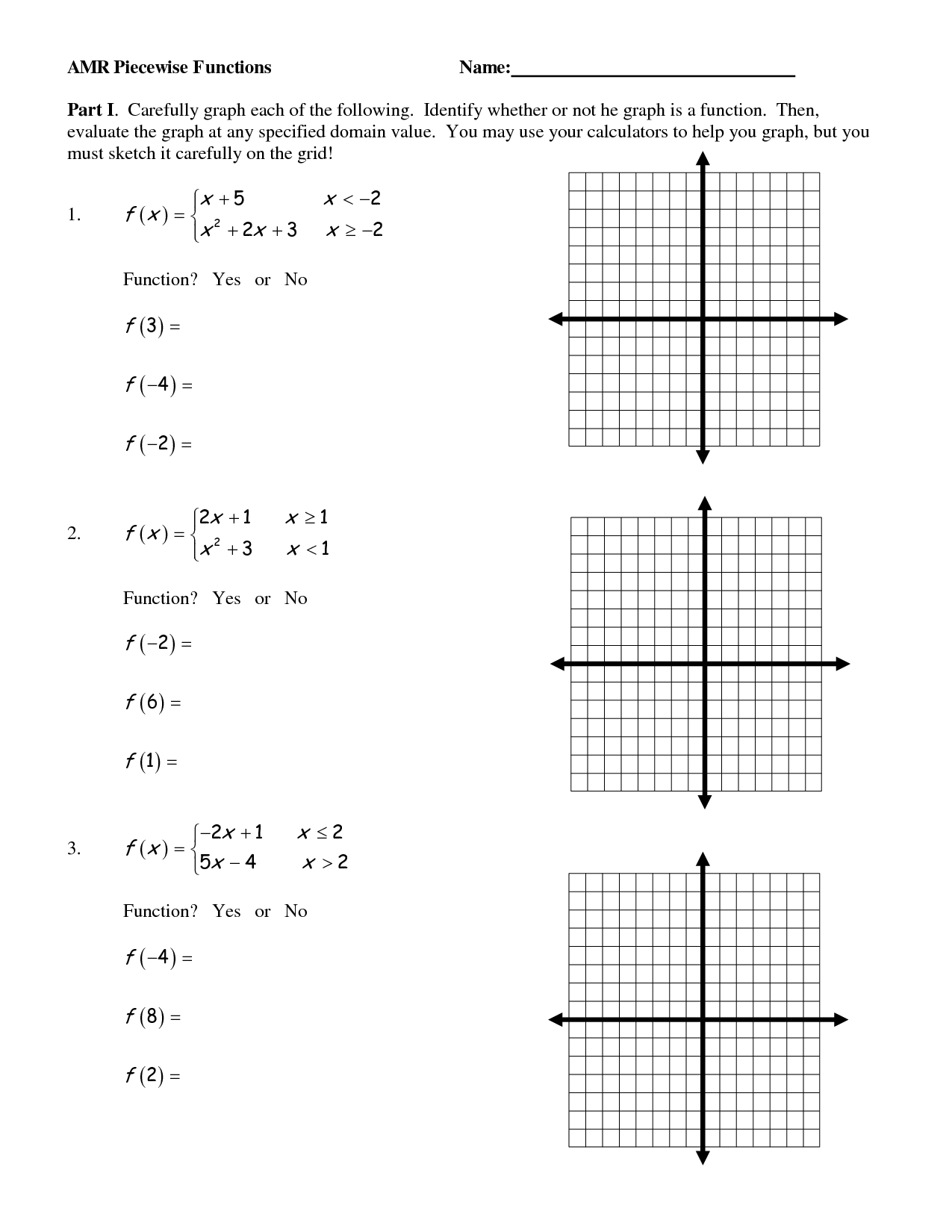
- Algebra 2 Piecewise Function Worksheets
- Piecewise Functions Worksheet
- Algebra 1 Worksheets
- Piecewise Functions Worksheet with Answers
- Algebra 1 Radicals Worksheet
- Graphing Polynomial Functions Worksheet
- Evaluating Algebra Expressions Worksheets
- Algebra 1 Linear Equation Worksheets
- Adding and Subtracting Radicals Worksheet
- Exponents Worksheets
- Algebra 1 Practice Worksheets
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Rosa Parks Worksheet Grade 1
What is the definition of a function?
A function is a relation between a set of inputs (called the domain) and a set of possible outputs (called the range), where each input is related to exactly one output. In other words, a function assigns exactly one output value for each input value. This fundamental concept is a key building block in mathematics and other fields, used to describe and analyze relationships between variables.
How do you evaluate a function for a specific value of the independent variable?
To evaluate a function for a specific value of the independent variable, you simply substitute that value into the function for the independent variable. For example, if you have a function f(x) and want to evaluate it at x = 3, you would substitute 3 into the function: f(3). Calculate the result of this substitution to find the value of the function at that specific point.
What is the difference between a dependent variable and an independent variable in a function?
In a function, the independent variable is the variable that the value of the function depends on, while the dependent variable is the variable which is determined by the value of the independent variable. The independent variable is the input, and the dependent variable is the output of the function.
What is the purpose of evaluating a function?
The purpose of evaluating a function is to determine the output value of the function for a given input value. By plugging in specific input values, we can calculate and understand how the function behaves, which can provide insights into its properties, behaviors, and relationships between different variables. This evaluation is essential for solving equations, analyzing patterns, making predictions, and drawing conclusions in various mathematical and scientific applications.
How do you determine the range of a function?
To determine the range of a function, you need to find all the possible output values that the function can produce when you input different values. One way to do this is by analyzing the behavior of the function and identifying the highest and lowest points it can reach. You can also graph the function and look at the vertical span of the graph to see the range of output values. In some cases, you may need to use algebraic techniques or mathematical properties specific to the function to determine its range.
What is the relationship between the graph of a function and its evaluation at specific values?
The graph of a function visually represents the relationship between the input values (x-axis) and the corresponding output values (y-axis) for that function. When evaluating a function at specific values, we are essentially determining the output value for a given input value. This means that the evaluation of a function at a specific value corresponds to finding the y-coordinate on the graph of the function for the corresponding x-coordinate. In other words, evaluating a function at a specific value allows us to determine where that point lies on the graph of the function.
How do you represent a function algebraically?
A function can be represented algebraically by using an equation or formula that relates the input variable, usually denoted as x, to the output variable, usually denoted as f(x). The function is typically written as f(x) = expression involving x, where the expression could involve various operations, constants, and variables.
What is the difference between an explicit and implicit function representation?
In an explicit function representation, the dependent variable is explicitly expressed in terms of the independent variable, providing a clear formula or equation that directly defines the relationship between the two variables. On the other hand, an implicit function representation does not have the dependent variable expressed explicitly in terms of the independent variable, often requiring additional steps to isolate the dependent variable. Implicit functions typically involve relationships that are not easily solvable for one variable in terms of the other, leading to more complex expressions.
How do you evaluate a composite function?
To evaluate a composite function, you need to substitute the inner function's input into the outer function. Start by evaluating the inner function first. Then take the result of the inner function and substitute it into the outer function. Finally, simplify the expression to get the final output of the composite function.
What does it mean for a function to be continuous?
A function is considered continuous if its values do not have abrupt changes or jumps, meaning that there are no gaps, holes, or breaks in its graph. In other words, a function is continuous if you can draw its graph without lifting your pencil from the paper. This implies that the function is smooth and connected, with a consistent behavior throughout its domain.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.















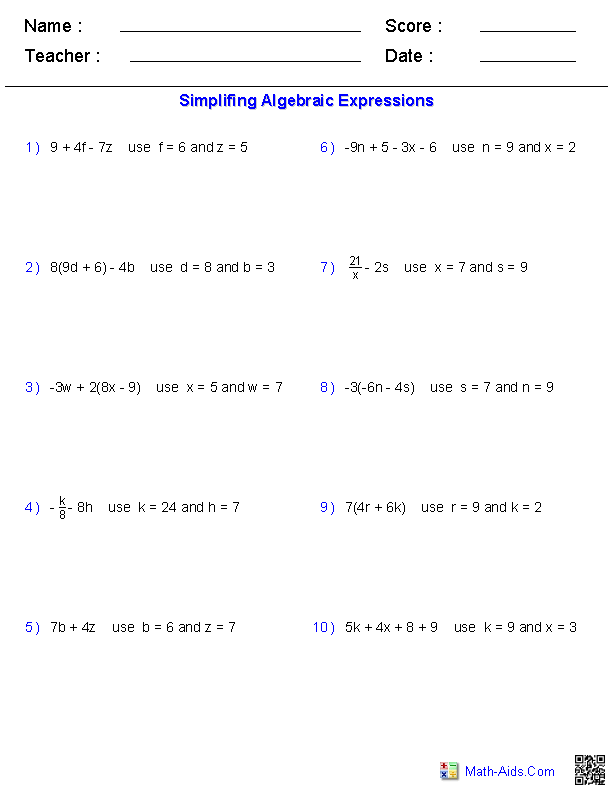


















Comments