Equations with Distributive Worksheet
Equations with distributive property can be a challenging topic for students learning algebra. It involves breaking down expressions and simplifying them using the distributive property. This worksheet is designed to provide practice problems and reinforce the concept of equations with distributive property. Whether you are a math teacher looking for additional resources or a student needing extra practice, this worksheet will help strengthen your understanding of this important algebraic concept.
Table of Images 👆
- Easy Distributive Property Worksheets
- Pre-Algebra Solving Equations Worksheets
- 6th Grade Math Worksheets Algebra
- Multi-Step Equations Worksheets
- Algebra 1 Worksheets
- 2 Step Equations Practice
- Multiplication and Division Worksheets 3rd Grade
- 6th Grade Math Word Problems Worksheets
- 8th Grade Math Word Problem Worksheets
- Factoring Trinomials Worksheet Answer Key
- Simplifying Algebraic Expressions Worksheet
- Dividing Fractions by Whole Numbers Models Worksheet
- Order of Operations Worksheets 5th Grade Math
- Algebra Math Worksheets Printable
- Algebra Math Worksheets Printable
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Rosa Parks Worksheet Grade 1
What is the basic principle of the distributive property?
The basic principle of the distributive property is that it allows you to distribute a factor across the terms inside a parenthesis in a mathematical expression. This means that you can multiply a sum by a factor by multiplying each term inside the parenthesis by that factor separately. In essence, the distributive property shows the relationship between multiplication and addition, enabling simplification and manipulation of algebraic expressions.
How can the distributive property be used to simplify expressions?
The distributive property allows us to efficiently multiply a single term by two or more terms inside a set of parentheses. By distributing the term, we can simplify the expression by multiplying each term inside the parentheses by the single term and then combining like terms. This property helps in breaking down complex expressions into simpler forms, making calculations easier and quicker.
How can the distributive property be used to expand expressions?
The distributive property can be used to expand expressions by multiplying each term inside the parentheses by the term outside the parentheses and then combining like terms. For example, in the expression 3(x + 4), you distribute the 3 to both the x and the 4 inside the parentheses by multiplying 3*x + 3*4, which results in 3x + 12. This method is helpful for simplifying and solving algebraic equations by breaking down the expression into simpler terms.
What is the role of parentheses in using the distributive property?
Parentheses are used in the distributive property to indicate that the operations inside the parentheses should be distributed across the terms outside the parentheses. This means that each term inside the parentheses is multiplied by each term outside the parentheses. Parentheses help emphasize the correct order of operations and ensure that the distributive property is applied correctly to simplify expressions.
Can the distributive property be applied with both addition and multiplication?
Yes, the distributive property can be applied with both addition and multiplication. When distributing with addition, you multiply each addend in the parentheses by the outside number. When distributing with multiplication, you multiply each factor within the parentheses by the outside number. This property helps simplify expressions and is a fundamental concept in algebra.
How does the distributive property help in solving equations?
The distributive property allows us to easily expand and simplify expressions by distributing a factor to each term inside parentheses. This property is extremely useful in solving equations as it helps us combine like terms, isolate variables and ultimately find solutions to the equations. By leveraging the distributive property, we can manipulate and transform equations to make them easier to solve and understand.
What are some common mistakes to avoid when using the distributive property?
Some common mistakes to avoid when using the distributive property include incorrectly distributing the terms, not applying the property to every term in the expression, forgetting to combine like terms after distributing, and overlooking negative signs when distributing to a negative term. It is important to carefully apply the distributive property to each term in the expression and ensure that all calculations are accurate to avoid errors.
Can the distributive property be applied to variables and constants?
Yes, the distributive property can be applied to both variables and constants. This property states that for any real numbers a, b, and c, the product of a and the sum (or difference) of b and c is equal to the sum (or difference) of the products of a and b, and a and c. This holds true regardless of whether a, b, or c are constants or variables.
How does the distributive property relate to combining like terms?
The distributive property is a math rule that states a(b + c) equals ab + ac. When combining like terms in algebra, you use the distributive property to simplify expressions by distributing a coefficient across terms inside parentheses before combining like terms. This allows you to efficiently simplify and solve algebraic equations by grouping and adding together terms with the same variables or exponents.
Are there any special cases where the distributive property applies differently?
Yes, the distributive property may apply differently when working with operations beyond addition and multiplication, such as division or exponentiation. Additionally, when dealing with non-commutative operations, the order of the terms in the equation can affect how the distributive property is applied. It's important to understand the specific properties and behaviors of the operations involved when applying the distributive property in various mathematical contexts.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.













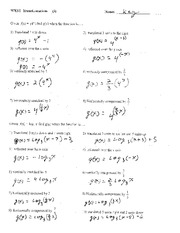

















Comments