Distributive Property with Fractions Worksheets
The distributive property is an important concept in mathematics, and understanding it can greatly enhance your ability to solve problems involving fractions. If you are a student or a parent looking for worksheets that specifically focus on the distributive property with fractions, you've come to the right place. In this blog post, we will explore the benefits of using worksheets that cater to this specific topic and provide you with the necessary practice to master the concept.
Table of Images 👆
- Distributive Property Math Algebra Worksheets
- Distributive Property Worksheets with Multiplication
- Distributive Property Math Algebra Worksheets
- Distributive Property Multiplication Worksheets
- Middle School Math Word Problems
- Simplifying Expressions Worksheets 7th Grade
- Simplifying Expressions Worksheets 7th Grade
- Solving Equations with Fractions Worksheet
- Equations with Distributive Property Worksheet
- Distributive Property Multiplication Coloring Page
- Distributive Property Worksheets 3rd Grade
- Distributive Property Worksheets
- Distributive Property Worksheets 4th Grade
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Rosa Parks Worksheet Grade 1
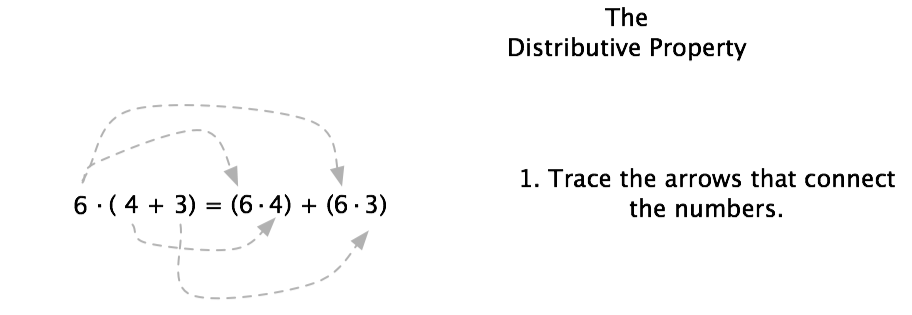
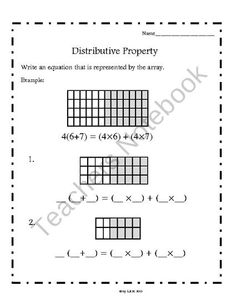
What is the distributive property?
The distributive property in mathematics states that multiplying a sum by a number is the same as multiplying each addend in the sum by the number and then adding the products together. Formally, it can be expressed as a(b + c) = ab + ac, where a, b, and c are any real numbers. This property is fundamental in algebra and is commonly used to simplify expressions and equations.
How does the distributive property apply to fractions?
The distributive property can be applied to fractions by multiplying the number outside the parentheses by each fraction inside the parentheses. For example, if you have the expression 3(1/2 + 1/3), you can distribute the 3 to both fractions inside the parentheses to get 3 * 1/2 + 3 * 1/3, which simplifies to 3/2 + 1. By applying the distributive property to fractions in this way, you can simplify expressions and perform operations more easily.
Give an example of using the distributive property with fractions.
One example of using the distributive property with fractions is as follows: (1/2) * (3/4 + 1/4). Using the distributive property, you can distribute the 1/2 to each term inside the parentheses, resulting in (1/2 * 3/4) + (1/2 * 1/4). This simplifies to (3/8) + (1/8), which equals 4/8 or 1/2.
How can the distributive property help simplify calculations with fractions?
The distributive property allows us to multiply a number by each part of a sum or difference within parentheses, which can be helpful when working with fractions. By applying the distributive property, we can simplify calculations with fractions by distributing the multiplication across terms in parentheses and then combining like terms to reduce the expression. This can make calculations more efficient and easier to manage, ultimately leading to simpler fraction computations.
How do you apply the distributive property when multiplying a fraction by a whole number?
To apply the distributive property when multiplying a fraction by a whole number, you simply multiply the whole number by the numerator of the fraction to get a new numerator, while keeping the same denominator. For example, when multiplying 3/4 by 5, you can distribute the multiplication as (3 * 5) / 4 = 15/4. This simplifies the multiplication process and helps in getting the final result efficiently.
Can you use the distributive property to simplify addition or subtraction with fractions?
Yes, the distributive property can be used to simplify addition or subtraction with fractions. When adding or subtracting fractions, the distributive property allows you to distribute the numerator or denominator of a fraction across the terms inside the parentheses before performing the arithmetic operation. This can help simplify the expression by combining like terms and making the computation more manageable.
How does the distributive property help in solving equations involving fractions?
The distributive property helps in solving equations involving fractions by allowing you to distribute or multiply a fraction across terms within parentheses. This enables you to simplify expressions, combine like terms, and isolate the variable when solving equations with fractions. By applying the distributive property correctly, you can effectively manipulate and rearrange the equation to find the value of the variable.
What are some common errors or misconceptions when using the distributive property with fractions?
One common error when using the distributive property with fractions is applying the property incorrectly, such as incorrectly distributing the fraction across addition or subtraction instead of multiplication. Another misconception is not simplifying the fractions before distributing, leading to incorrect results. It is important to remember to always distribute fractions by multiplying the fraction by the number outside the parentheses and then simplify the result if needed to avoid errors.
Can the distributive property be used with mixed numbers or improper fractions?
Yes, the distributive property can be used with both mixed numbers and improper fractions. When using the distributive property with mixed numbers, convert the mixed numbers into improper fractions before applying the property. The distribution process remains the same regardless of whether you are working with whole numbers, fractions, mixed numbers, or improper fractions.
How can practicing distributive property with fractions help improve overall math skills?
Practicing the distributive property with fractions can help improve overall math skills by enhancing understanding of how fractions can be combined and simplified in more complex equations. It improves proficiency in multiplication, division, addition, and subtraction of fractions, which are fundamental skills in various mathematical concepts. Additionally, it fosters critical thinking and problem-solving abilities by requiring students to break down problems into smaller, manageable steps and apply the distributive property methodically. This practice can also boost confidence in handling fractions and manipulating equations, leading to a deeper comprehension of mathematical principles and better performance in more challenging math problems.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.

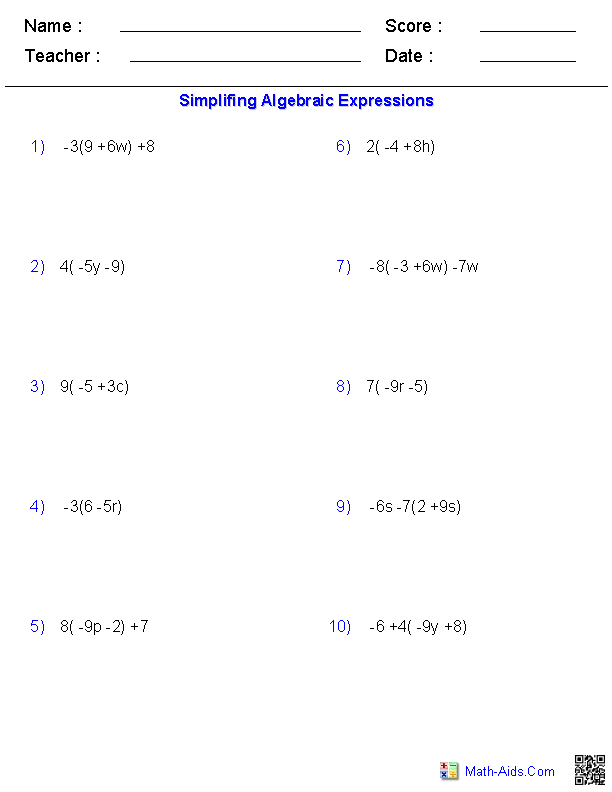



























Comments