Congruent Similar Polygons Worksheet

📆 Updated: 1 Jan 1970
👥 Author: James Lee
🔖 Category: Other
💭 Comments

Are you a math teacher or a student looking for a comprehensive resource on congruent and similar polygons? Look no further! We have created a helpful congruent similar polygons worksheet that will allow you to practice and master the concepts of congruence and similarity in polygons. This worksheet is designed to cater to both teachers who need a tool for classroom instruction and students who are looking for additional practice outside of the classroom. With a variety of engaging problems and clear explanations, this worksheet is perfect for anyone looking to enhance their understanding of congruent and similar polygons.

Congruent Worksheets 3rd Grade

Similar Figures Examples

2-Dimensional Shapes Worksheets

Free Printable Triangle Shapes

More Other Worksheets

Kindergarten Worksheet My Room
Spanish Verb Worksheets
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Art Handouts and Worksheets
7 Elements of Art Worksheets

What is the definition of congruent polygons?

Congruent polygons are geometric figures that have the same size and shape. This means that all corresponding sides are of equal length, and all corresponding angles are equal in measure. Ultimately, congruent polygons can be superimposed on top of each other perfectly, without any gaps or overlaps.

How can you prove that two polygons are congruent?

Two polygons are congruent if all corresponding sides are equal in length and all corresponding angles are equal in measure. In order to prove that two polygons are congruent, you can show that their corresponding sides and angles match up either through the use of side-side-side (SSS), side-angle-side (SAS), angle-side-angle (ASA), angle-angle-side (AAS), or angle-angle-angle (AAA) congruence criteria. By demonstrating that these criteria are met, you can conclude that the two polygons are congruent.

What are the properties of congruent polygons?

Congruent polygons have the same shape and size, which means that their corresponding sides are equal in length and their corresponding angles are equal in measurement. Additionally, congruent polygons can be superimposed on top of each other, with their corresponding sides and angles perfectly overlapping. This property allows us to prove that two polygons are congruent by showing that all their corresponding sides and angles are equal.

How are angles affected in congruent polygons?

In congruent polygons, the angles are the same in measure and are positioned in corresponding locations. This means that if two polygons are congruent, then their corresponding angles are equal in size. So, congruent polygons have the same angles, even though their sides may be of different lengths or in different orientations.

How are side lengths affected in congruent polygons?

In congruent polygons, the corresponding sides have the same length. This means that the side lengths of congruent polygons are equal, and the polygons have the same shape and size when superimposed on each other.

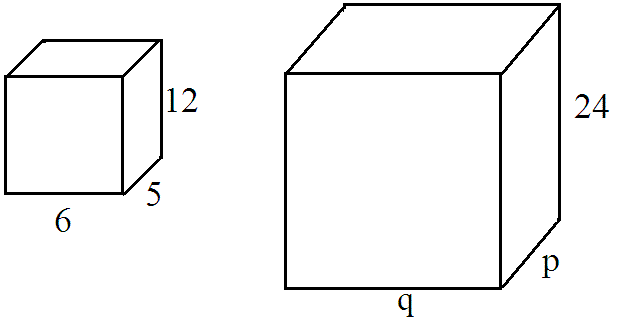
What is the definition of similar polygons?

Similar polygons are polygons that have the same shape but are not necessarily the same size. This means that corresponding angles of similar polygons are equal and corresponding sides are in proportion to each other.

How can you prove that two polygons are similar?

Two polygons are considered similar if their corresponding angles are congruent and their corresponding sides are in proportion to each other. To prove that two polygons are similar, you can show that all corresponding angles are equal by measuring them or using geometric theorems, and then demonstrate that the ratios of their corresponding sides are equal. This can be done by comparing the lengths of corresponding sides and showing that they maintain the same ratio across the polygons.

What are the properties of similar polygons?

Similar polygons have corresponding angles that are congruent and corresponding sides that are in proportion to each other. This means that the ratios of the corresponding side lengths of similar polygons are equal. Additionally, the scale factor, which is the ratio of the lengths of corresponding sides, is the same for all pairs of corresponding sides.

How are angles affected in similar polygons?

In similar polygons, the corresponding angles are congruent, which means they have the same measure. This property holds true for all pairs of corresponding angles in similar polygons, regardless of the size or scale of the polygons. Therefore, the angles in similar polygons are directly proportional, maintaining their relationship as the polygons are scaled up or down.

How are side lengths affected in similar polygons?

In similar polygons, the side lengths are proportional to each other. This means that if two polygons are similar, corresponding sides of the polygons are in the same ratio. For example, if the ratio of the side lengths of two similar polygons is 2:1, then one side of the larger polygon is twice the length of the corresponding side in the smaller polygon. This property allows us to determine the relationship between the side lengths of similar polygons and understand how they are related to each other.

Some of informations, names, images and video detail mentioned are the property of their respective owners & source.

Have something to share?

Comments

Who is Worksheeto?

At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.