Congruent Figures Worksheets

Congruent figures worksheets provide a valuable tool for educators and students alike to reinforce their understanding of this important geometric concept. With a focus on identifying and comparing figures that have the same shape and size, these worksheets cater to learners who need further practice in recognizing congruence in various contexts. From elementary school students just starting to explore geometry to middle schoolers expanding their knowledge, these worksheets offer a comprehensive selection of exercises that target this specific subject, allowing learners to strengthen their grasp of congruence in a structured and engaging way.

  Congruent Triangles Worksheet

---

  Similar Figures Worksheet

---

  Non Congruent Shapes Worksheets

---

  Triangle Meaning

---

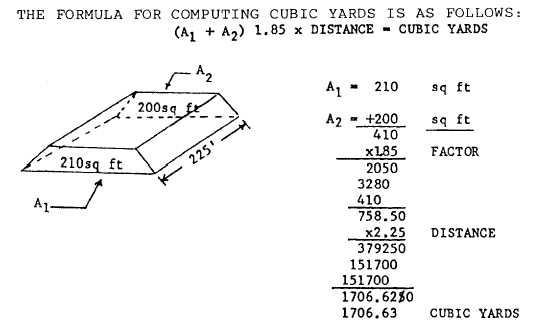
  How to Figure Cubic Yards of Concrete

---

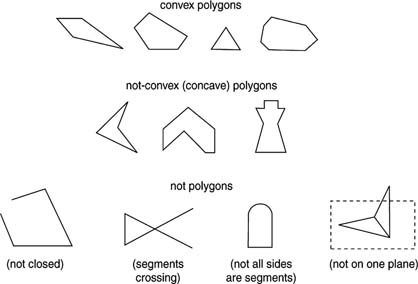
  What Is a Non Polygon

---

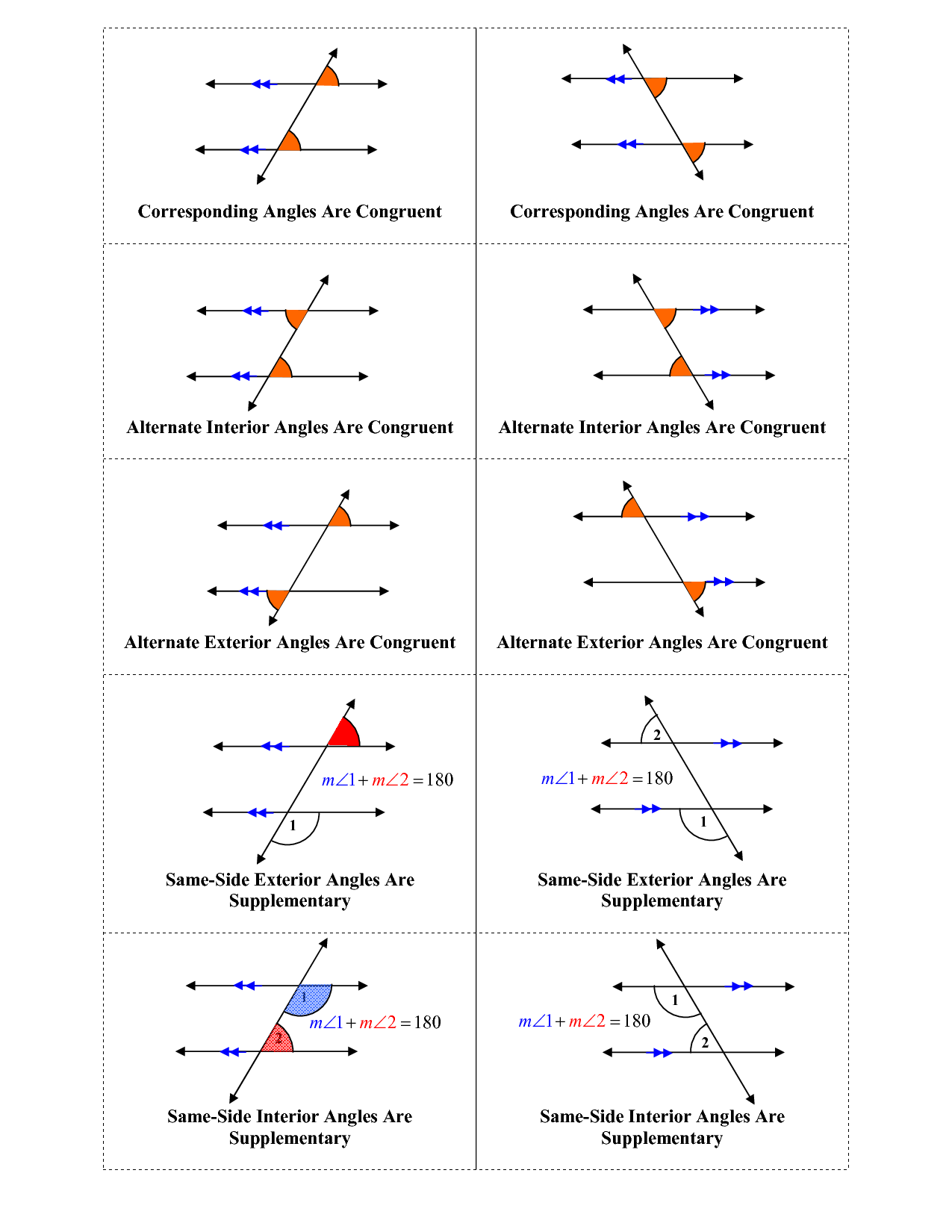
  Corresponding and Alternate Interior Angles

---

  Line and Angle Relationships Worksheet

---

  Drawing Congruent Shapes Worksheets

---

  Drawing Congruent Shapes Worksheets

---

What are congruent figures worksheets?

Congruent figures worksheets are educational resources that provide exercises for students to practice identifying and working with congruent shapes. These worksheets typically include questions that involve determining if shapes are congruent, matching congruent figures, and solving problems that require an understanding of congruence properties such as side lengths and angles. By engaging with these worksheets, students can enhance their skills in geometry and develop a solid understanding of congruence in geometric figures.

How are congruent figures defined in geometry?

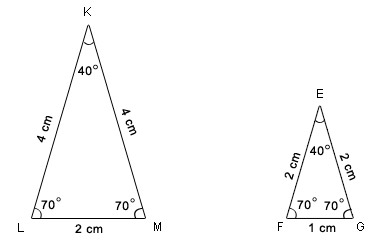
Congruent figures in geometry are defined as shapes or objects that have the same size and shape, where corresponding angles are equal and corresponding sides are of equal length. Two figures are considered congruent if they can be transformed into each other through a combination of translations, rotations, and reflections without changing their size or shape.

Why is it important to determine if figures are congruent?

It is important to determine if figures are congruent because congruent figures have identical shape and size, meaning their corresponding sides and angles are equal. Understanding congruence helps in various applications such as geometry, architecture, engineering, and design to ensure accuracy and precision in measuring and constructing shapes. Identifying congruent figures also allows for making accurate comparisons and predictions in mathematical and practical scenarios.

What are some key properties of congruent figures?

Congruent figures have the same shape and size, with corresponding sides and angles that are equal in measure. This means that if you were to superimpose one figure on top of the other, they would align perfectly without any gaps or overlaps. Congruent figures can be transformed through translations, rotations, and reflections while preserving their congruency.

How do you prove that two figures are congruent?

Two figures are proven to be congruent when all of their corresponding sides are equal in length and all of their corresponding angles are equal in measure. This can be demonstrated by using geometric tools such as rulers and protractors to measure the sides and angles of each figure, and showing that they are identical in size and shape. Additionally, congruence can also be proven by using certain congruence postulates and theorems, such as Side-Angle-Side (SAS), Side-Side-Side (SSS), Angle-Side-Angle (ASA), and Angle-Angle-Side (AAS), which state specific conditions under which two figures are guaranteed to be congruent.

What are some common ways to visually represent congruent figures?

Some common ways to visually represent congruent figures include overlapping images of the same figure, using different colors or patterns to show the similarity, showing corresponding angles and sides are equal in length, and using notation such as marking tick marks or congruence symbols on corresponding angles and sides.

How does the concept of congruent figures relate to transformations in geometry?

Congruent figures in geometry are shapes that have the same size and shape. When we apply transformations such as translations, rotations, reflections, or dilations to a figure, the resulting figure is still congruent to the original figure. This is because the transformations preserve the size and shape of the figures, maintaining their congruency. So, the concept of congruent figures is closely related to transformations in geometry as they help us understand how figures can change position or orientation while still maintaining their original size and shape.

What are some real-life applications of congruent figures?

Real-life applications of congruent figures include architecture, where congruent shapes are used to design buildings with symmetry and balance; in manufacturing, where congruent figures are used to ensure precision and accuracy in the production of products; in urban planning, where congruent shapes are used to design road layouts and city structures for efficiency and functionality; and in art and design, where congruent figures are used to create patterns and decorations that are visually pleasing and aesthetically satisfying.

Can congruent figures have different orientations or positions?

Yes, congruent figures can have different orientations or positions. Congruent figures are identical in size and shape, but they can be rotated, reflected, or translated in space while maintaining their congruent properties. Thus, even though the orientation or position of congruent figures may differ, they are still considered congruent.

How do congruent figures worksheets help students develop problem-solving skills in geometry?

Congruent figures worksheets help students develop problem-solving skills in geometry by providing them with opportunities to analyze and compare shapes in different orientations, sizes, and positions. Students have to recognize similarities and differences between shapes to determine if they are congruent, enabling them to understand geometric relationships and properties. By working through these worksheets, students also practice applying spatial reasoning and critical thinking skills to solve problems involving congruency, which ultimately strengthens their overall problem-solving abilities in geometry.