Comparing Fractions Worksheets 2nd Grade

Fractions can be a tricky concept for young learners, but with the right practice, they can become masters in no time! If you're searching for worksheets that will engage second-grade students while reinforcing their understanding of comparing fractions, you're in luck. In this blog post, we'll explore a variety of worksheets that focus on this essential math skill.

  Comparing Fractions Worksheets 4th Grade

---

  Comparing Fractions Worksheet 5th Grade

---

  Ordering Fractions and Decimals Worksheets

---

  Integers Greater than Less than Worksheets

---

  Comparing Fractions Worksheet 7th Grade

---

  2nd Grade Math Worksheets Fractions

---

  Equivalent Fractions Worksheets 6th Grade

---

  Comparing Fractions Worksheets

---

  Comparing Fractions 3rd Grade Math Worksheets

---

  Printable Fraction Worksheets 2nd Grade Math

---

  Comparing Fractions Worksheets 3rd Grade

---

  5th Grade Math Fraction Models Worksheets

---

  Comparing Unit Fractions Worksheet

---

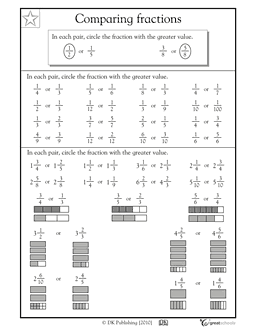
How can you determine which fraction is larger: ½ or ¾?

To determine which fraction is larger between ½ and ¾, you can compare their numerators. In this case, the numerator of ¾ (3) is greater than the numerator of ½ (1). Therefore, ¾ is larger than ½.

Compare the fractions 3/4 and 2/5. Which fraction is larger?

To compare the fractions 3/4 and 2/5, you can convert them to have a common denominator. Both fractions can be converted to have a denominator of 20 by multiplying the first fraction by 5/5 and the second fraction by 4/4, resulting in 15/20 for 3/4 and 8/20 for 2/5. Therefore, 3/4 is larger than 2/5.

Which fraction is smaller: 2/3 or 4/5?

The fraction 2/3 is smaller than 4/5 because when comparing fractions, the larger the denominator, the smaller the fraction. In this case, the fraction with the larger denominator, 4/5, is greater than the fraction with the smaller denominator, 2/3.

Compare the fractions 1/3 and 5/6. Which fraction is larger?

The fraction 5/6 is larger than 1/3. This can be determined by finding a common denominator, which in this case is 6. When both fractions are expressed with a denominator of 6, 1/3 becomes 2/6 and 5/6 remains the same. Therefore, 5/6 is larger than 1/3.

Which fraction is smaller: 7/8 or 4/5?

Out of 7/8 and 4/5, 7/8 is smaller.

Compare the fractions 2/6 and 1/3. Which fraction is larger?

To compare fractions, we can convert them to have the same denominator. Both 2/6 and 1/3 can be written with a denominator of 6. 2/6 is equivalent to 2/6, while 1/3 is equivalent to 2/6. Therefore, 1/3 (which is equivalent to 2/6) is larger than 2/6.

Which fraction is smaller: 3/7 or 4/9?

The fraction 3/7 is smaller than 4/9 because when comparing fractions, we can cross multiply to compare the values of the fractions - in this case, 3*9 (27) < 4*7 (28), meaning 3/7 is smaller than 4/9.

Compare the fractions 5/10 and 3/8. Which fraction is larger?

To compare 5/10 and 3/8, we need to find a common denominator. Both fractions can be written with a denominator of 40. 5/10 is equivalent to 20/40, and 3/8 is equivalent to 15/40. Therefore, 20/40 (or 5/10) is larger than 15/40 (or 3/8).

Which fraction is smaller: 2/5 or 4/9?

The fraction 2/5 is smaller than 4/9.

Compare the fractions 3/6 and 1/2. Which fraction is larger?

The fractions 3/6 and 1/2 are equivalent. They both represent the same value of 0.5 or 50%. Therefore, neither fraction is larger than the other as they are equal.