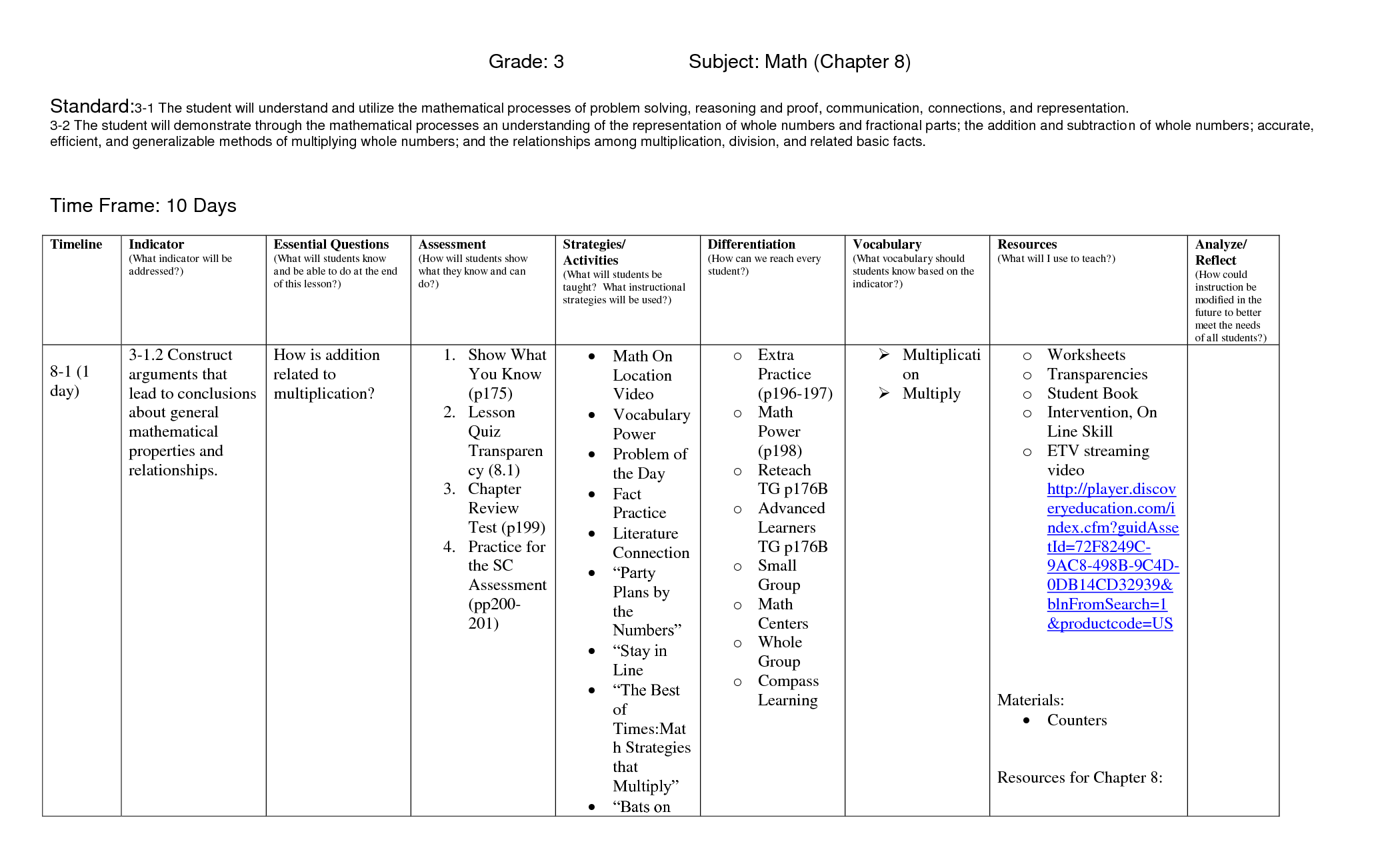
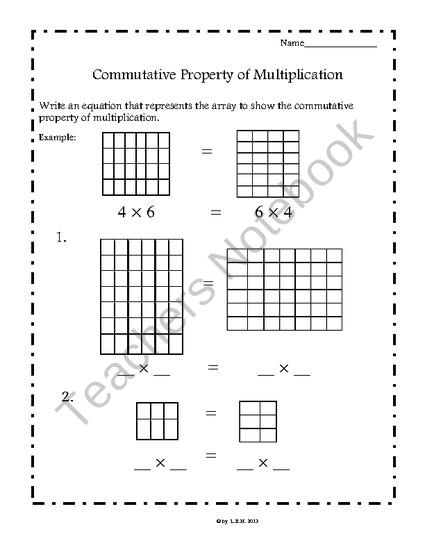
Commutative Property of Multiplication Worksheets

The Commutative Property of Multiplication is an important concept in basic arithmetic. These worksheets are designed to help students understand and practice this property, ensuring a solid foundation in mathematics.

  Commutative Property of Addition Worksheets 3rd Grade

---

  Commutative and Associative Properties Worksheets

---

  Commutative Property Multiplication Worksheet

---

  Multiplication Properties Worksheet

---

  Commutative Property Multiplication Worksheet

---

  Commutative Property Multiplication Worksheets 3rd Grade

---

  Commutative Property Worksheets

---

  Inverse Property of Multiplication Worksheets

---

  Associative Property of Multiplication Definition

---

  3rd Grade Multiplication Properties Worksheet

---

  Distributive Property Multiplication Worksheets

---

  Commutative and Associative Properties Worksheets

---

  Addition Properties Worksheet

---

What is the commutative property of multiplication?

The commutative property of multiplication states that the order of the factors in a multiplication equation can be changed without affecting the product. In other words, for any two numbers a and b, a * b = b * a. This property allows for the factors to be rearranged, while still yielding the same result.

How does the commutative property affect the order of multiplication?

The commutative property states that changing the order of the factors in a multiplication equation does not change the result. This means that when applying the commutative property to multiplication, the order of the factors can be rearranged without affecting the outcome. For example, in the equation 2 x 3 x 4, the order of multiplication can be rearranged to 4 x 3 x 2, and the result will still be the same (24).

Can you provide an example of the commutative property of multiplication in action?

Yes, an example of the commutative property of multiplication is: 2 x 3 = 3 x 2. This demonstrates that no matter the order in which the numbers are multiplied, the result remains the same, proving the commutative property of multiplication.

How does the commutative property relate to the order of factors in a multiplication problem?

The commutative property in multiplication states that changing the order of factors does not change the product. This means that for any two numbers being multiplied, the result will be the same regardless of the order in which they are multiplied. In other words, when applying the commutative property to a multiplication problem, you can rearrange the factors without affecting the outcome.

Does the commutative property work for all numbers and multiplication problems?

Yes, the commutative property holds true for all numbers and multiplication problems. This property states that changing the order of the numbers being multiplied does not change the result, meaning that a x b = b x a for any numbers a and b.

What happens when you switch the places of the factors in a multiplication problem using the commutative property?

When you switch the places of the factors in a multiplication problem using the commutative property, the result remains the same. This property states that changing the order of the numbers being multiplied does not change the final product. For example, if you are multiplying 2 x 3, you will get 6. If you switch the places of the factors to 3 x 2, you will still get 6 as the answer.

Can you give an example where the commutative property of multiplication is not applicable?

In the context of matrix multiplication, the commutative property does not hold. For example, if we have two matrices A and B, such that A is a 2x3 matrix and B is a 3x2 matrix, AB is defined and has different dimensions than BA. As a result, the order of multiplication is significant in matrix multiplication, making it non-commutative.

How does the commutative property make multiplication more efficient?

The commutative property states that changing the order of operands does not change the result of the operation. In the context of multiplication, this means that you can multiply numbers in any order and still get the same result. This property makes multiplication more efficient because you can choose the order that makes the calculation easier or faster for you, without affecting the final outcome. It allows for flexibility in how you approach and solve multiplication problems, ultimately saving time and effort.

Why is the commutative property an important concept in mathematics?

The commutative property is important in mathematics because it allows us to reorder the numbers in an operation without changing the result. This property simplifies calculations and proofs, making it easier to work with various mathematical operations. It is fundamental in algebra, arithmetic, and geometry, providing a key property that is widely applicable across different mathematical disciplines.

How does the commutative property relate to other mathematical operations?

The commutative property states that changing the order of two numbers being added or multiplied does not change the result. This property is closely related to addition and multiplication operations. It does not hold for subtraction and division, meaning the order in which numbers are subtracted or divided matters and can change the result. Therefore, the commutative property specifically applies to addition and multiplication operations, while subtraction and division do not follow this property.