Calculus Review Worksheet

A calculus review worksheet is a helpful tool for students who want to reinforce their understanding of key concepts and practice problem-solving skills. Whether you are a high school student preparing for an AP calculus exam or a college student looking to brush up on your calculus skills, these worksheets serve as a structured resource to help you solidify your knowledge and master the subject.

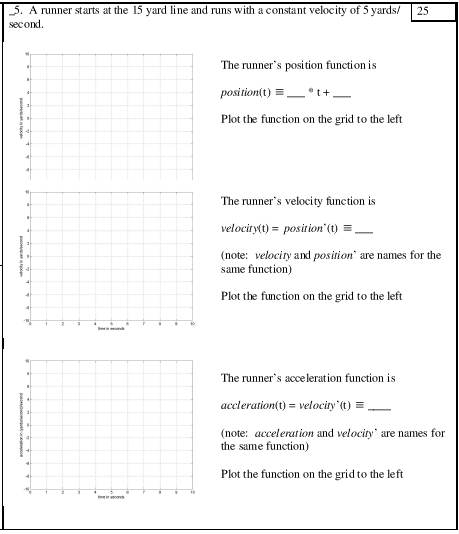
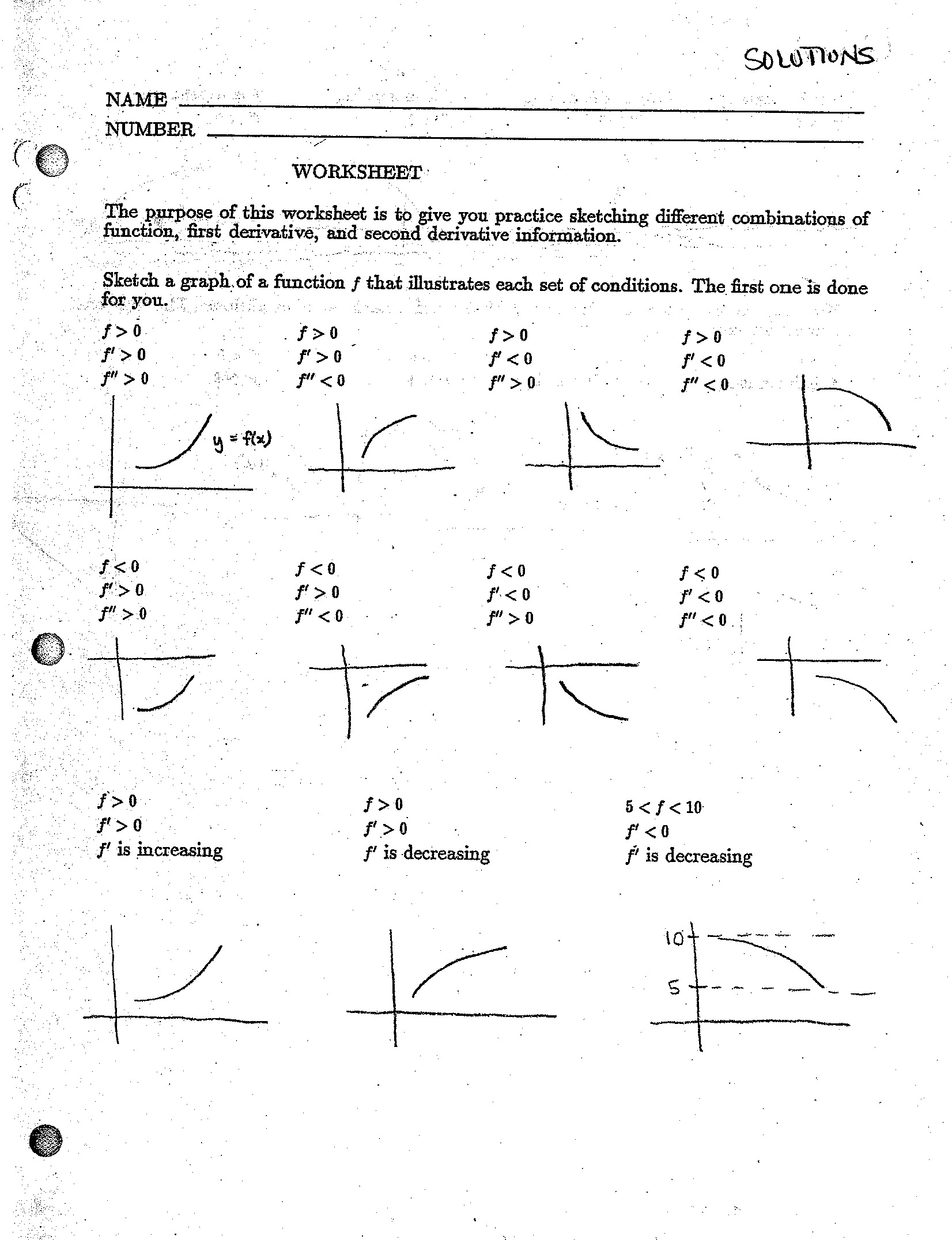
  Example Calculus Worksheets

---

  Function Transformation Worksheet

---

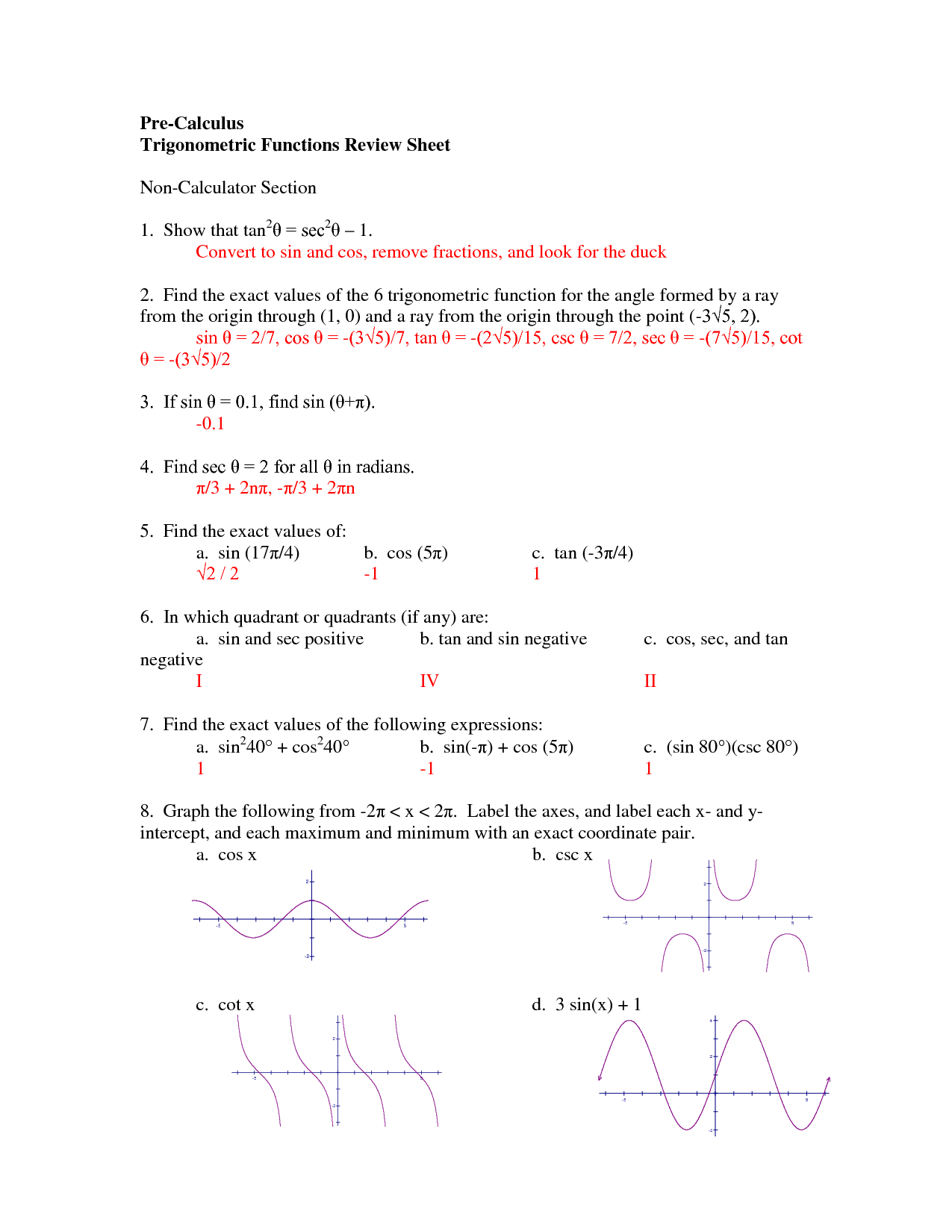
  Review for Pre Calculus Trig Identities Worksheet

---

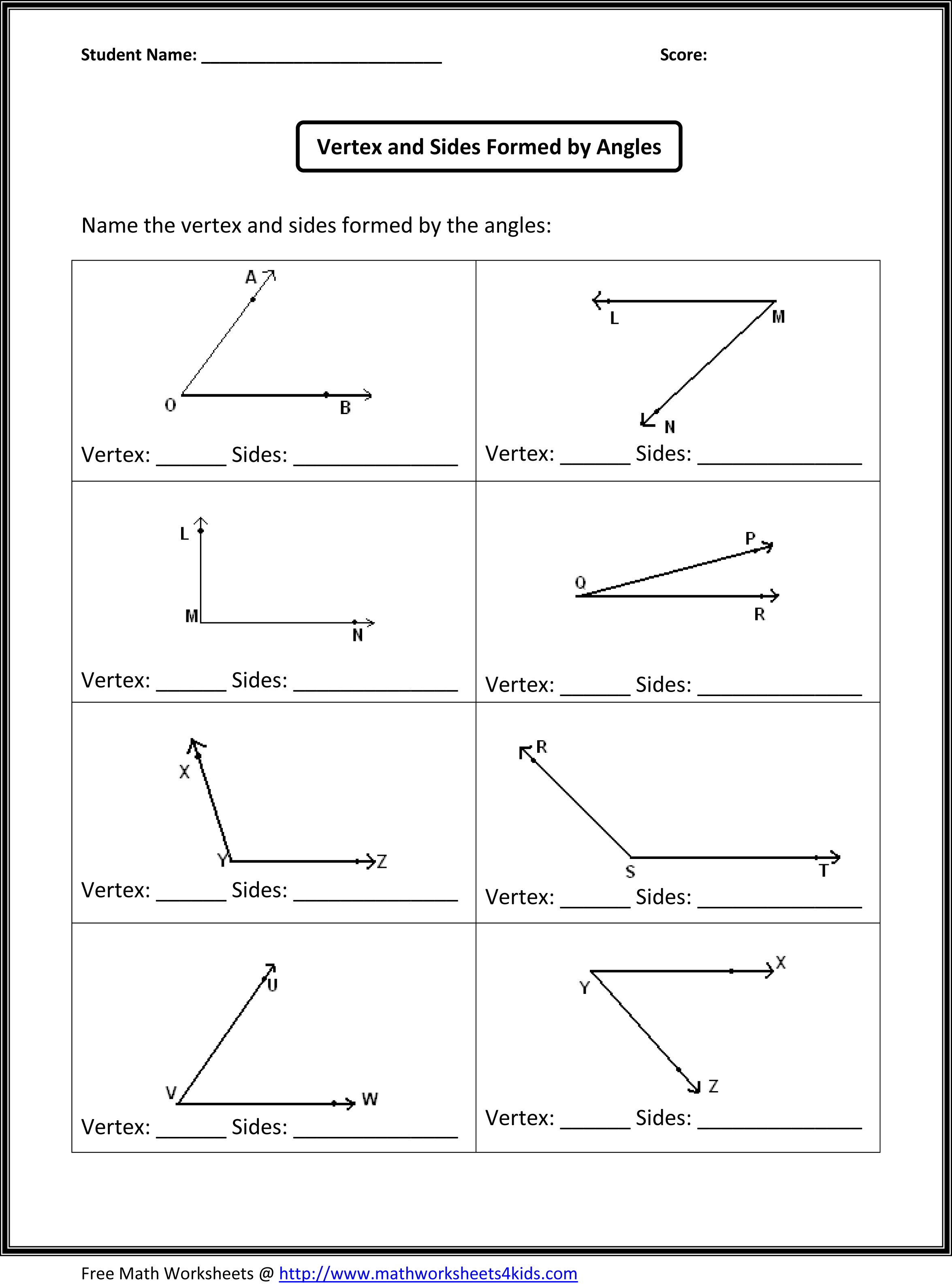
  Geometry Angles Worksheet 4th Grade

---

  System of Inequalities Worksheet Answers Unit 5

---

  Stem and Leaf Plot Worksheets 6th Grade

---

  Piecewise Functions Worksheet with Answers

---

  Vector Calculus Cheat Sheet

---

  Trig Functions Worksheet

---

  College Math Homework Worksheets

---

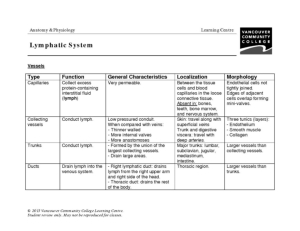
  Lymphatic System Worksheet

---

  Printable Computer Lab Worksheets

---

  Calvin and Hobbes Math Atheist

---

  P1 P2 P3

---

  Kindergarten Math Subtraction

---

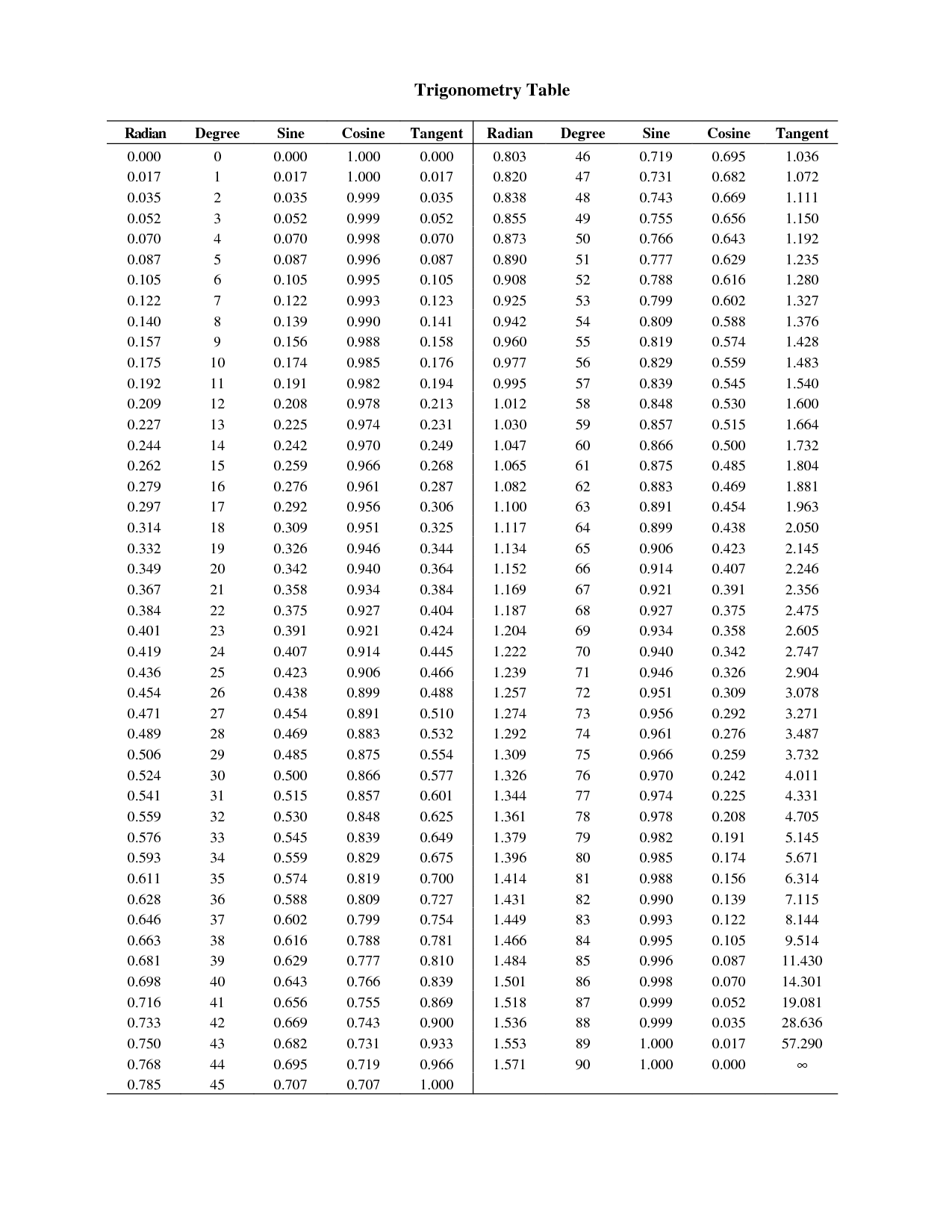
  Sine Cosine Tangent Unit Chart

---

  Sine Cosine Tangent Unit Chart

---

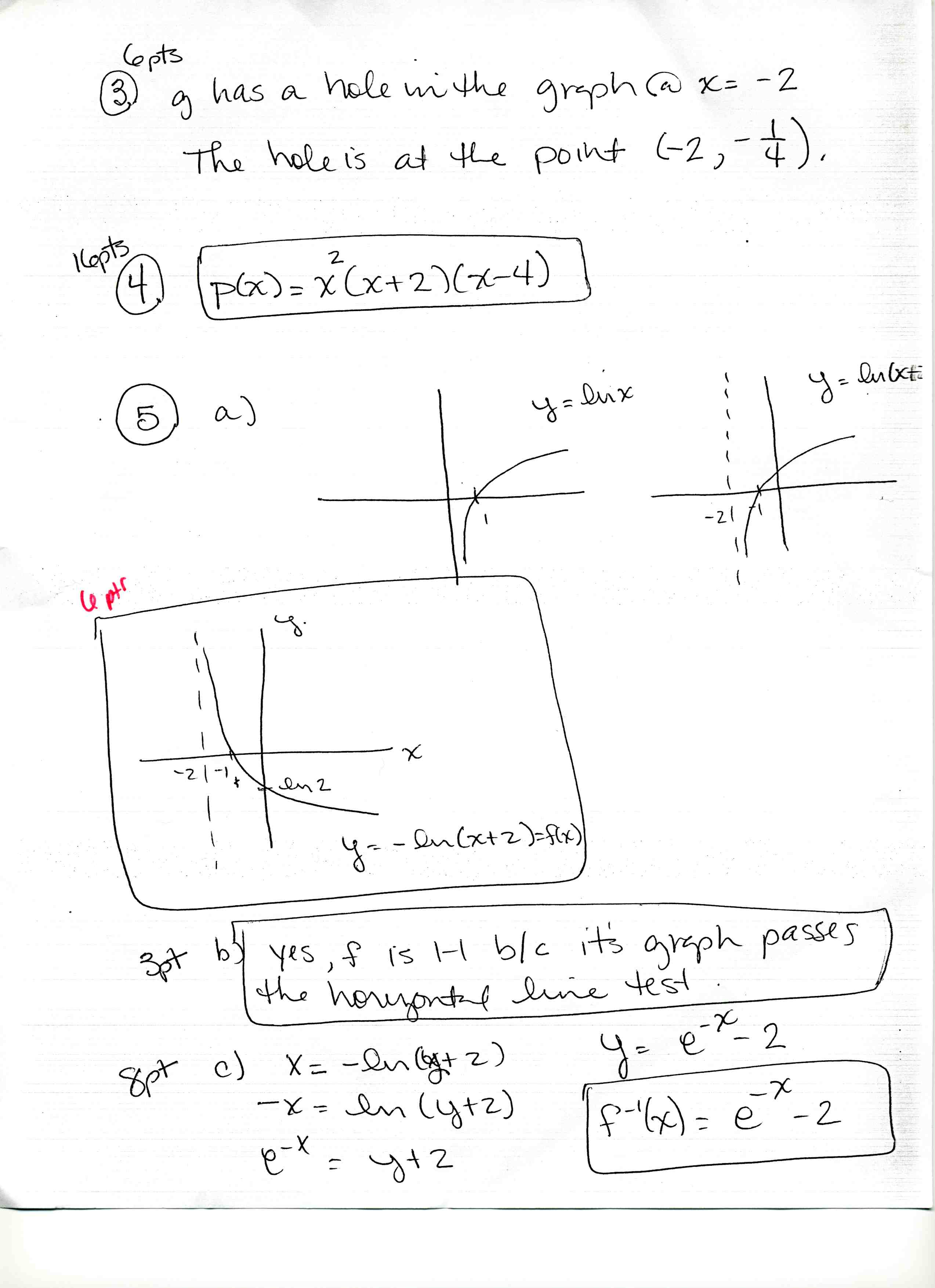
What is the definition of a derivative?

A derivative is a financial instrument whose value is derived from the value of an underlying asset, index, or interest rate. It allows investors to speculate on the price movements of the underlying asset without owning it directly, providing opportunities for hedging, leveraging, and risk management in financial markets.

How do you find the derivative of a constant function?

The derivative of a constant function is always 0. This is because the rate of change of a constant function is constant, which means there is no change in the function itself. Therefore, when you differentiate a constant function, you always get 0 as the result.

What is the product rule in calculus?

The product rule in calculus is a formula used to find the derivative of the product of two functions. It states that if you have two functions, f(x) and g(x), the derivative of the product f(x) * g(x) is equal to the derivative of the first function times the second function, plus the first function times the derivative of the second function. Mathematically, it can be written as (f(x) * g(x))' = f'(x) * g(x) + f(x) * g'(x).

How do you find the derivative of a trigonometric function?

To find the derivative of a trigonometric function, you apply the rules of differentiation, such as the chain rule and the derivative formulas for trigonometric functions. Each trigonometric function has a specific derivative formula. For example, the derivative of sine is cosine and the derivative of cosine is negative sine. By identifying the function you are differentiating and applying the appropriate derivative formula, you can find the derivative of a trigonometric function.

What is the chain rule and how is it used?

The chain rule in calculus is a method for finding the derivative of a composite function. It states that when two functions are composed together, the derivative of the composite function is the product of the derivative of the outer function and the derivative of the inner function. In other words, it allows us to find the rate of change of a function that is composed of multiple functions by breaking it down into smaller, more manageable parts. The chain rule is essential in calculating derivatives of complex functions and is widely used in various fields such as physics, engineering, and economics.

How do you find critical points of a function?

To find the critical points of a function, you need to first find the derivative of the function and set it equal to zero. Solve this equation to find the x-values of the critical points. These points are where the function may have a maximum, minimum, or point of inflection. Additionally, check the points where the derivative is undefined for critical points.

What is the definite integral of a function?

The definite integral of a function is a numerical value that represents the signed area under the curve of the function over a specified interval. It is essentially finding the limit of Riemann sums as the width of the partitions approaches zero, which gives the exact area under the curve between two points on the x-axis.

How do you find the area under a curve using integrals?

To find the area under a curve using integrals, you first need to set up the integral of the function representing the curve over the interval of interest. This involves integrating the function with respect to the variable of integration within the specified interval. The definite integral gives you the net area between the curve and the x-axis over that interval. By evaluating this integral, you can find the area under the curve.

What is the fundamental theorem of calculus?

The fundamental theorem of calculus states that differentiation and integration are inverse operations of each other. In simpler terms, it explains that finding the area under a curve (integration) and finding the rate of change of that area (differentiation) are closely related and can be used interchangeably.

How can you use calculus to determine the maximum or minimum values of a function?

To determine the maximum or minimum values of a function using calculus, you would first find the derivative of the function. Then, set the derivative equal to zero to find the critical points. Next, use the second derivative test or first derivative test to determine if the critical points are maximum, minimum, or neither. The critical points that yield the highest value are the maximum values, and the critical points that yield the lowest value are the minimum values of the function.