Associative Properties Worksheets
Are you searching for engaging worksheets that can help reinforce the concept of associative properties? Look no further! In this blog post, we will provide you with a range of carefully designed worksheets suitable for students in elementary and middle school. These worksheets are an excellent tool for teachers and parents who want to help their students develop a strong understanding of how numbers can be grouped and multiplied.
Table of Images 👆
- Addition Properties 3rd Grade Worksheets
- Commutative and Associative Properties Worksheets
- Properties of Real Numbers Worksheet.pdf
- Commutative Property Multiplication
- Identity Property of Addition Worksheets
- Multiplication 3rd Grade Math Distributive Properties
- Distributive Property of Multiplication 3rd
- Glencoe Algebra 2 Answer Key Chapter 4
- Writing Algebraic Expressions Worksheets
- Writing Algebraic Expressions Worksheets
- Writing Algebraic Expressions Worksheets
- Writing Algebraic Expressions Worksheets
- Writing Algebraic Expressions Worksheets
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Art Handouts and Worksheets
7 Elements of Art Worksheets
What is the associative property of addition?
The associative property of addition states that changing the grouping of numbers being added does not change the sum. In other words, when adding three or more numbers, the sum remains the same regardless of how the numbers are grouped together. This property allows us to regroup numbers in different ways while performing addition without affecting the final result.
What is the associative property of multiplication?
The associative property of multiplication states that when multiplying three or more numbers, the way in which the numbers are grouped does not change the result. In mathematical terms, it means that (a * b) * c is equal to a * (b * c) for any numbers a, b, and c. This property allows us to change the grouping of factors when multiplying without changing the final product.
How does the associative property apply to addition of three or more numbers?
The associative property states that the way in which numbers are grouped doesn't change the result of addition. When adding three or more numbers, you can group them in any way you like and the result will be the same. For example, when adding 1 + 2 + 3, you can add 1 + 2 first, followed by 3, or you can add 2 + 3 first, followed by 1. Both ways will give you the same result of 6, illustrating the associative property of addition for three or more numbers.
How does the associative property apply to multiplication of three or more numbers?
The associative property states that when multiplying three or more numbers, the way in which the numbers are grouped does not affect the result. For example, when multiplying three numbers a, b, and c, (a * b) * c will give the same result as a * (b * c). This means that you can multiply the numbers in any order or group them however you like, and the final product will remain the same.
Give an example of using the associative property in an addition problem.
An example using the associative property in an addition problem would be: (2 + 3) + 4 = 2 + (3 + 4). This means that regardless of how the numbers are grouped with parentheses, the result of adding them together remains the same.
Give an example of using the associative property in a multiplication problem.
An example of using the associative property in a multiplication problem would be: (2 x 3) x 4 = 2 x (3 x 4). In this case, both sides of the equation result in the same answer of 24, demonstrating the associative property which states that changing the grouping of numbers being multiplied does not change the product.
How does the associative property help simplify calculations in mathematics?
The associative property allows us to change the grouping of numbers in an operation without changing the result. This property helps simplify calculations by allowing us to regroup numbers in a way that is easier to work with, making calculations more efficient and manageable. By rearranging the numbers, we can often make the calculation simpler and easier to perform, saving time and effort in solving mathematical problems.
Can the associative property be applied to any type of numbers or operations?
Yes, the associative property can be applied to any type of numbers or operations. This property states that the way in which numbers are grouped in an operation does not affect the result. Therefore, it is applicable to addition, multiplication, and other operations with real numbers, integers, fractions, and even complex numbers.
Explain how the associative property is related to grouping numbers in parentheses.
The associative property states that the grouping of numbers does not affect the outcome of addition or multiplication. When we group numbers in parentheses, we are essentially creating a specific order of operations that ensures the associative property holds. By grouping numbers in parentheses, we can ensure that the numbers are added or multiplied in the intended order, regardless of how they are grouped, thus demonstrating the relationship between the associative property and grouping numbers in parentheses.
How does the associative property contribute to problem-solving skills in mathematics?
The associative property in mathematics allows us to change the grouping of operations without changing the result, which helps streamline calculations and simplify complex problems. By leveraging this property, problem solvers can rearrange numbers and operations to organize information more efficiently, leading to faster and more accurate solutions. This flexibility in grouping operations enhances critical thinking skills by encouraging students to approach problems from different perspectives and find alternative methods to reach the same outcome.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.







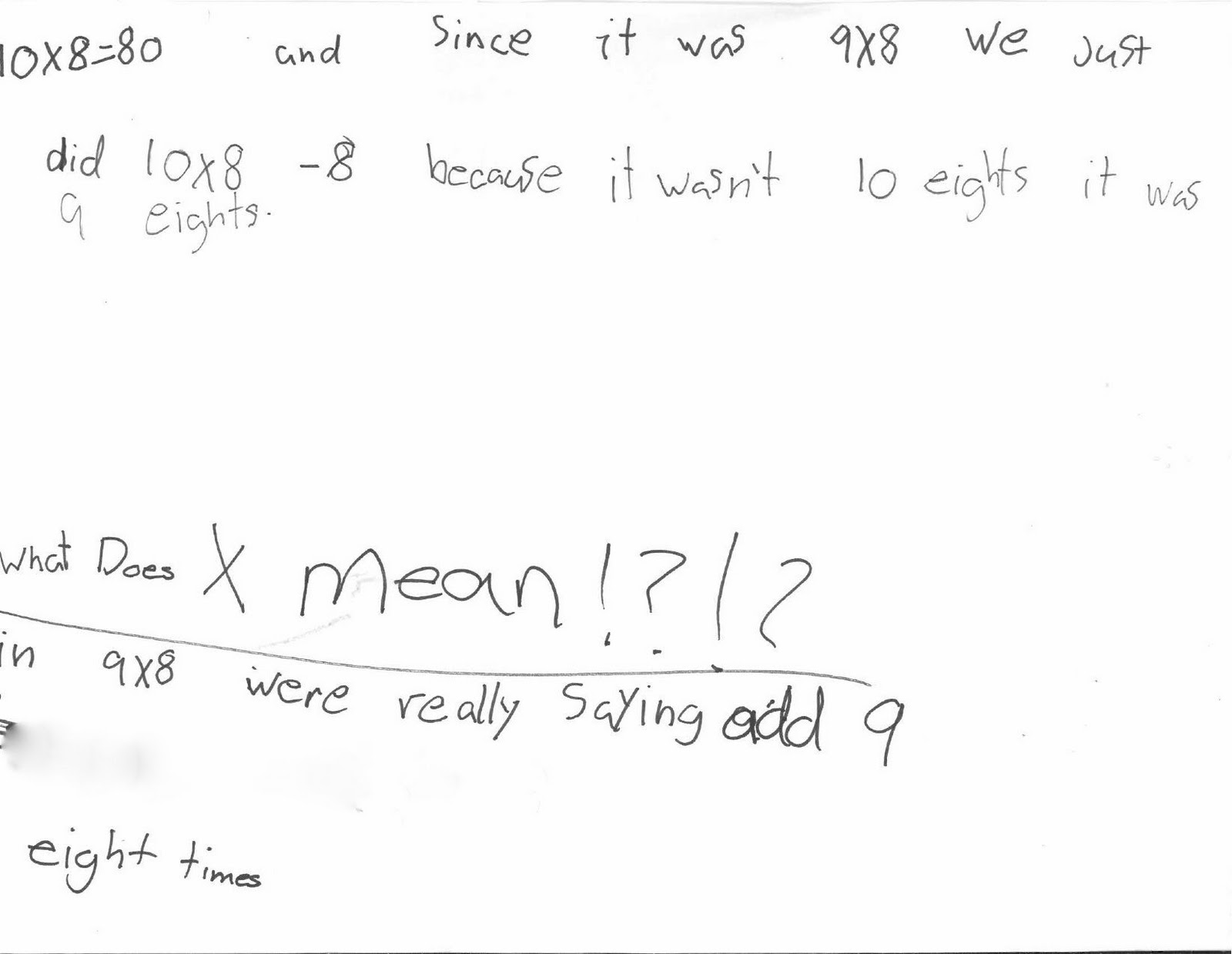





















Comments