Area of a Circle Worksheet
Are you interested in testing your knowledge of calculating the area of a circle? Look no further than our Area of a Circle Worksheet! This worksheet is designed for students who are learning about the concept of finding the area of a circle and want practice in solving related problems. With a variety of questions and exercises, this worksheet is the perfect tool to reinforce learning and gain confidence in working with these mathematical concepts.
Table of Images 👆
- Geometry Circle Worksheets
- 6th Grade Math Worksheet Circumference Area Circle S
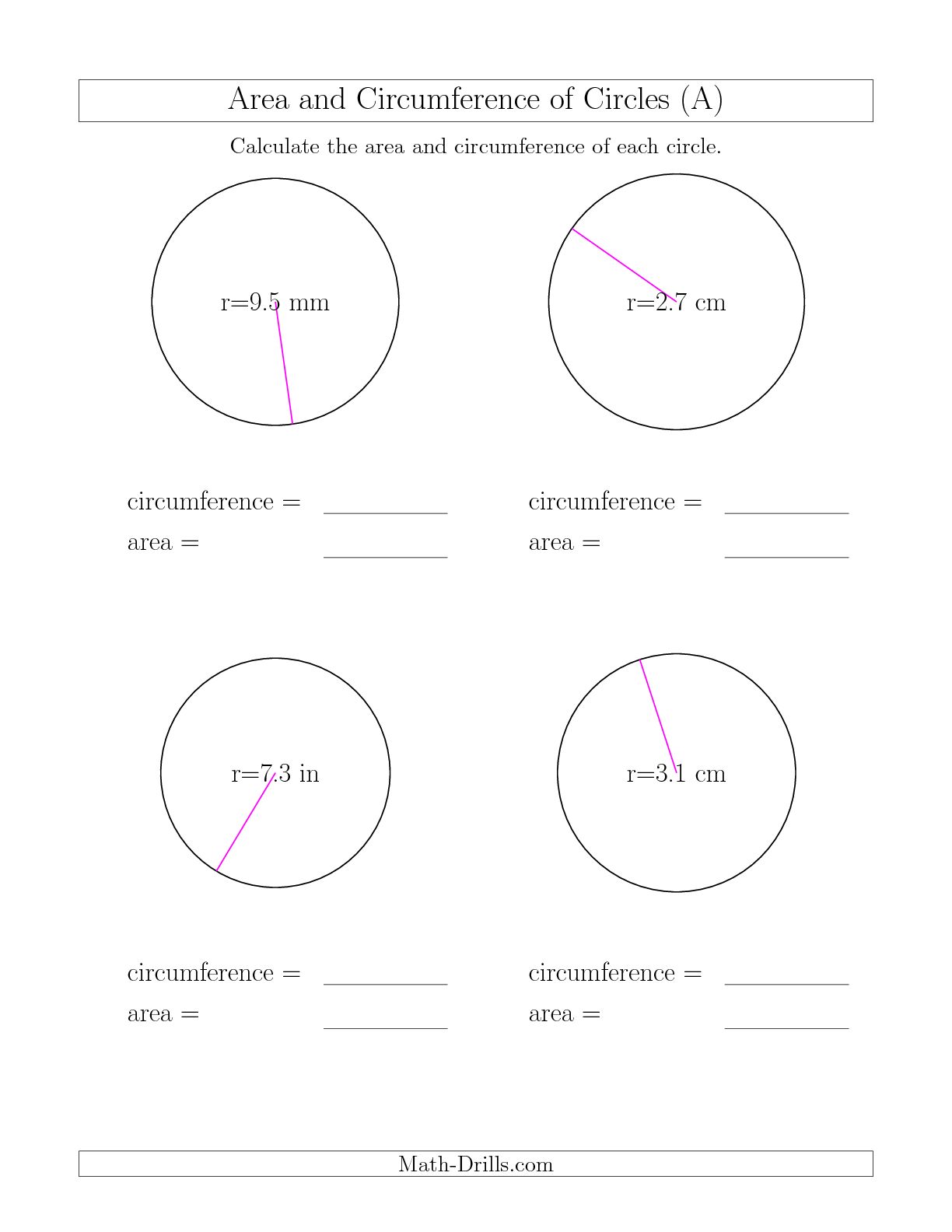
- Area Circumference Circle Worksheet
- Radius Circumference and Area of a Circle Worksheet
- Areas of Circles and Sectors Worksheet
- Trigonometry Unit Circle Worksheet
- Circle Circumference and Area Worksheet
- Circumference and Area Worksheets
- Arc Length Sector Circle Worksheet
- Radius and Diameter Worksheets
Geometry Circle Worksheets
6th Grade Math Worksheet Circumference Area Circle S
Area Circumference Circle Worksheet
Geometry Circle Worksheets
Radius Circumference and Area of a Circle Worksheet
Areas of Circles and Sectors Worksheet
Trigonometry Unit Circle Worksheet
Areas of Circles and Sectors Worksheet
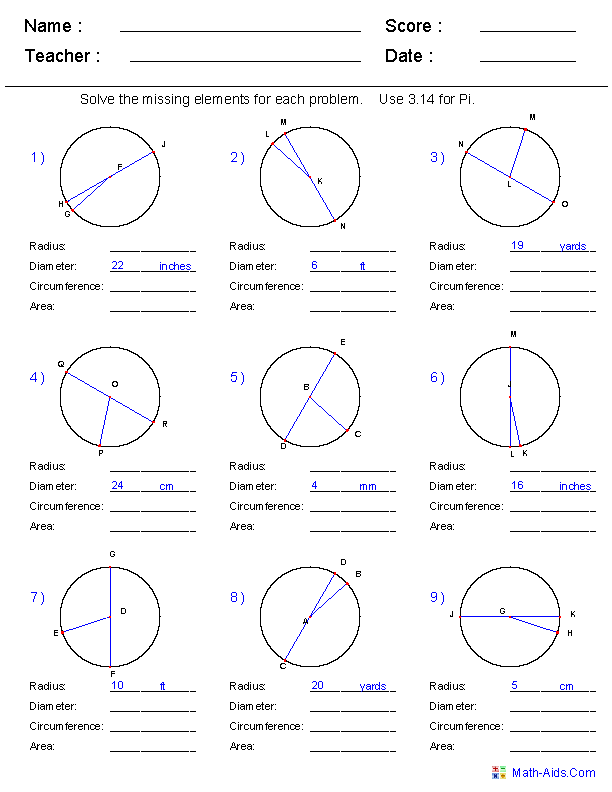
Circle Circumference and Area Worksheet
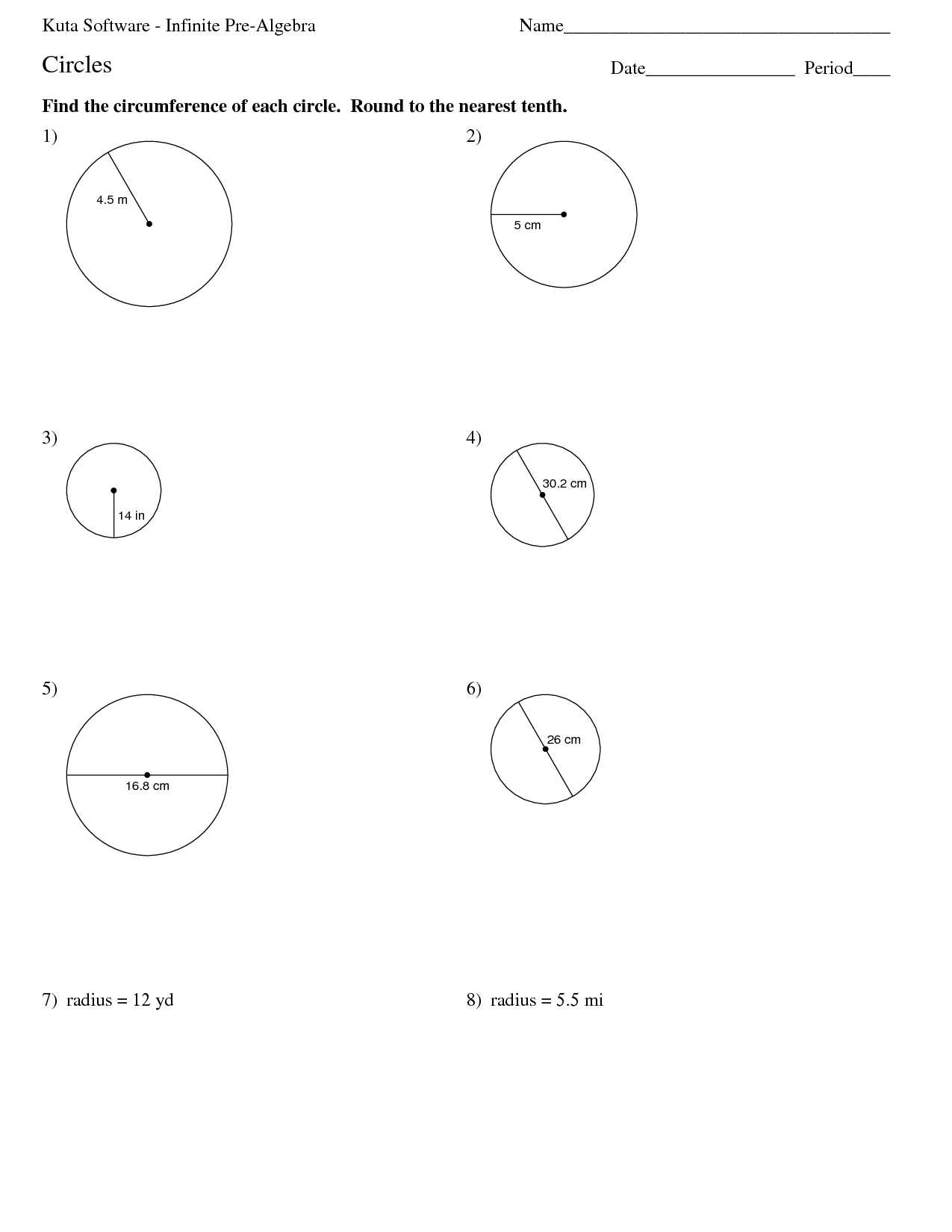
Circumference and Area Worksheets
Arc Length Sector Circle Worksheet
Areas of Circles and Sectors Worksheet
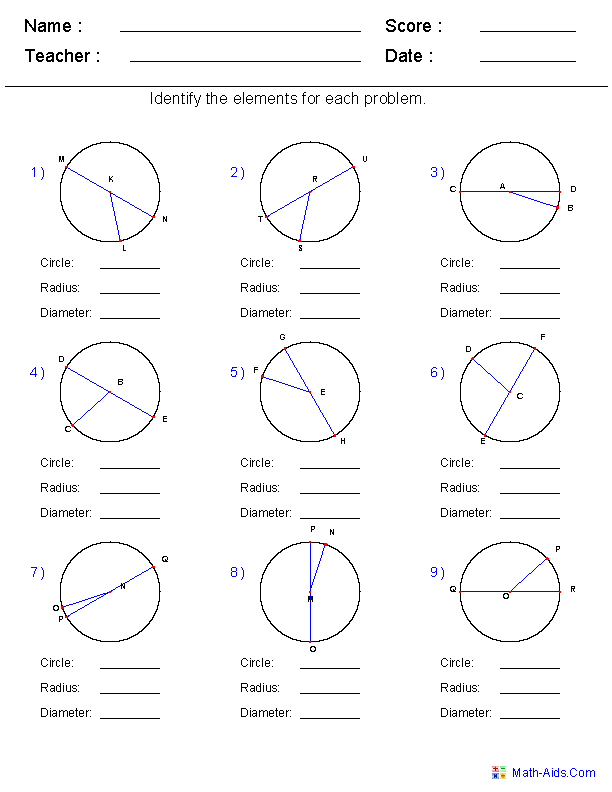
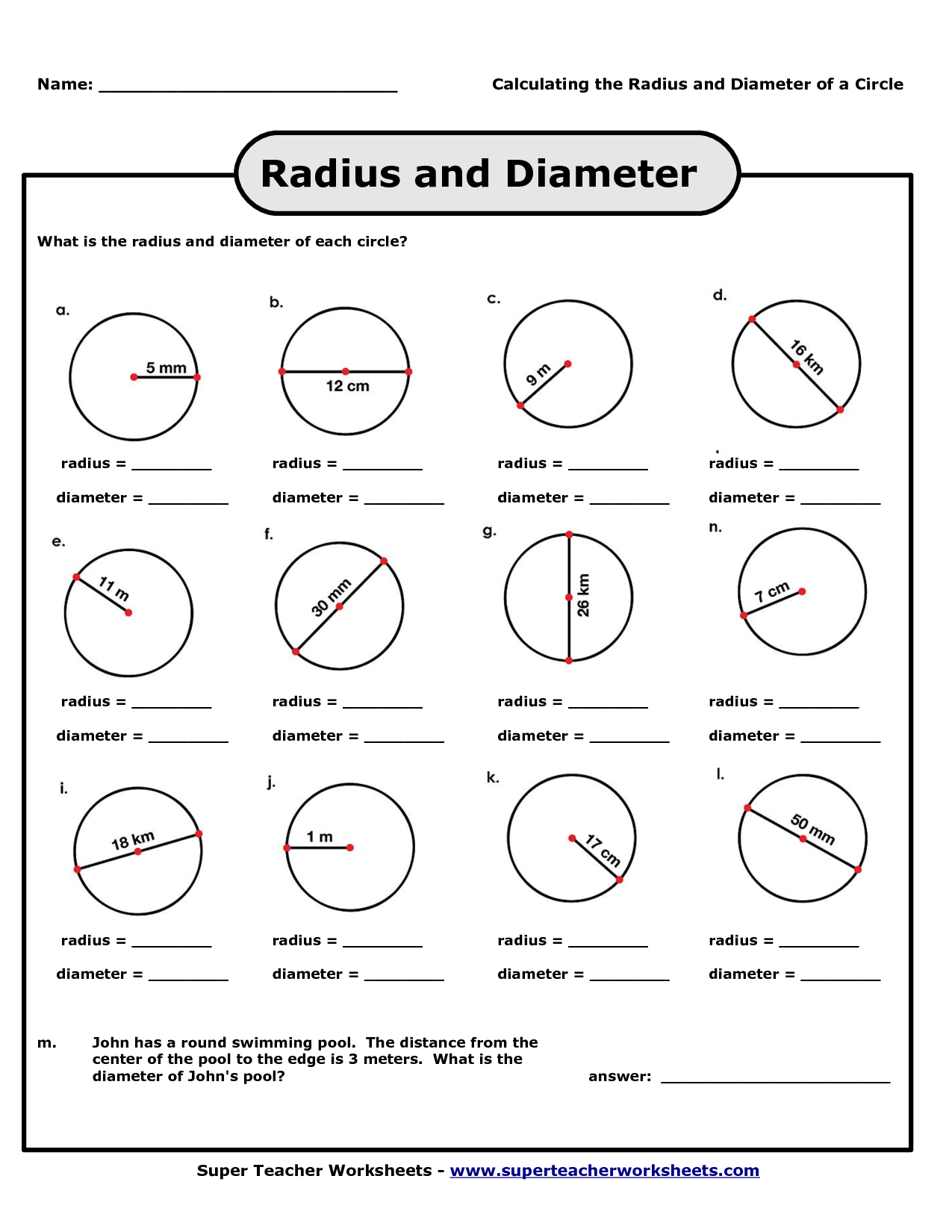
Radius and Diameter Worksheets
Area Circumference Circle Worksheet
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Cooking Vocabulary Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Art Handouts and Worksheets
7 Elements of Art Worksheets
All Amendment Worksheet
Symmetry Art Worksheets
Daily Meal Planning Worksheet
What is the formula for finding the area of a circle?
The formula for finding the area of a circle is A = ?r^2, where A is the area and r is the radius of the circle.
How is the radius of a circle related to its area?
The radius of a circle is directly related to its area. The area of a circle is calculated using the formula A = ?r^2, where A represents the area and r is the radius of the circle. This means that the area of a circle increases as the square of the radius. So, if the radius of a circle is doubled, the area will be four times greater, and if the radius is halved, the area will be one-fourth of the original area.
What unit is typically used to measure the area of a circle?
The unit typically used to measure the area of a circle is square units, such as square meters, square feet, or square centimeters.
If a circle has a diameter of 10 units, what is its radius?
The radius of a circle is half the length of its diameter, so if a circle has a diameter of 10 units, its radius would be 5 units.
How is the circumference of a circle related to its area?
The circumference of a circle is directly related to its diameter by the formula C = ?d, where C represents the circumference and d is the diameter of the circle. On the other hand, the area of a circle is related to its radius by the formula A = ?r^2, where A represents the area and r is the radius of the circle. Therefore, while the circumference of a circle is determined by its diameter, the area of a circle is determined by its radius.
Can the area of a circle ever be negative? Why or why not?
No, the area of a circle cannot be negative. The area of a circle is always a positive value because it represents the amount of space enclosed by the circle's boundary. The formula for calculating the area of a circle (?r^2) involves squaring the radius, which ensures that the result is always positive or zero. Negative values do not make sense in the context of measuring area, so a circle's area can never be negative.
How does the area of a circle change if its radius is doubled?
If the radius of a circle is doubled, the area of the circle will increase by a factor of four. This is because the area of a circle is proportional to the square of its radius. So, if the radius is doubled, the area of the circle will be four times larger than the original circle.
How does the area of a circle change if its radius is divided by 2?
If the radius of a circle is divided by 2, it means the new radius is half of the original radius. Since the area of a circle is calculated as ? times the square of the radius (A = ?r^2), if the radius is divided by 2, the new radius is (1/2)r. Thus, the new area of the circle would be (?*(1/2)^2)*r^2, which simplifies to 1/4 of the original area. Therefore, dividing the radius by 2 results in the area of the circle being reduced to 1/4 of its original value.
Explain how you would find the area of a circle with a given diameter.
To find the area of a circle with a given diameter, you first need to know the value of the diameter. Once you have the diameter, you can calculate the radius by dividing the diameter by 2. Then, use the formula for the area of a circle, which is ? times the radius squared (A = ?r^2), to find the area. Simply substitute the radius you calculated into the formula to determine the area of the circle.
What is the significance of the ratio of a circle's circumference to its diameter, often represented by the Greek letter pi (?)?
The significance of the ratio of a circle's circumference to its diameter, represented by the number pi (?), is that it is a constant value approximately equal to 3.14159. Pi is an irrational number, meaning it cannot be expressed as a simple fraction, and it is used in mathematics to calculate important geometric properties of circles and other curved shapes. Pi appears in various scientific and engineering applications, such as calculating the area of a circle or determining the volume of a sphere, making it a fundamental constant in mathematics.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.
Comments