Angles Word Problems Worksheets

Angles word problems worksheets are a valuable resource for students who are learning about geometry and need practice applying their knowledge of angles in real-life scenarios. These worksheets provide a variety of word problems that require students to identify and calculate different types of angles, such as acute, obtuse, and right angles. With these worksheets, students can develop their understanding of angles as an entity and apply their knowledge to solve problems involving angles as a subject.

  2nd Grade Math Word Problems Worksheets

---

  6th Grade Math Worksheets Angles

---

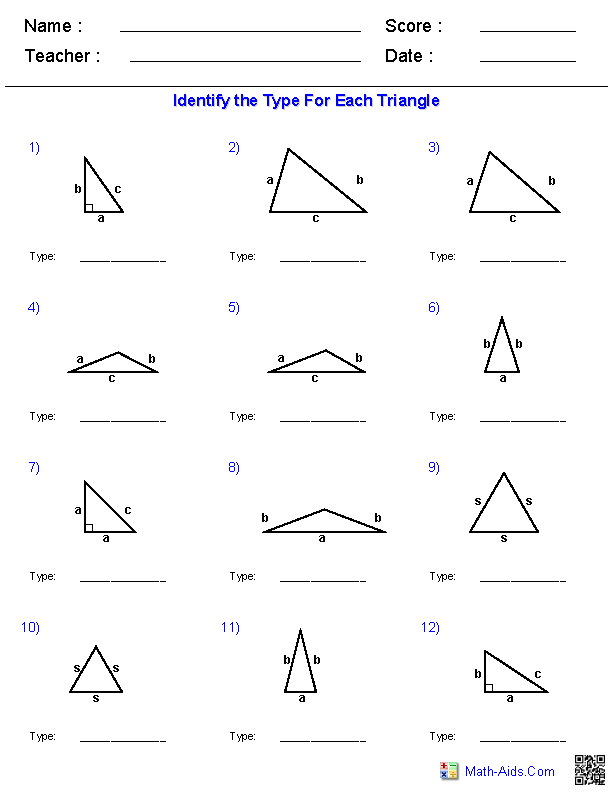
  Identifying Triangles Worksheets

---

  4th Grade Math Problems Worksheets

---

  6th Grade Ratio Worksheets

---

  8th Grade Math Worksheets Algebra

---

  Area Word Problems Worksheets

---

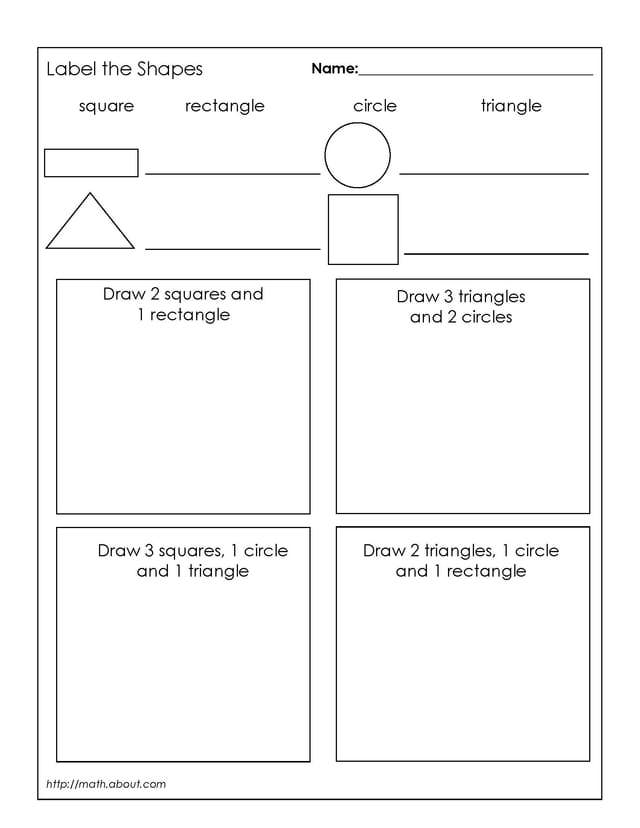
  Math Shapes Worksheets 1st Grade

---

  Ratio and Proportion Word Problems

---

  Alternate Interior Angles Exterior Worksheet

---

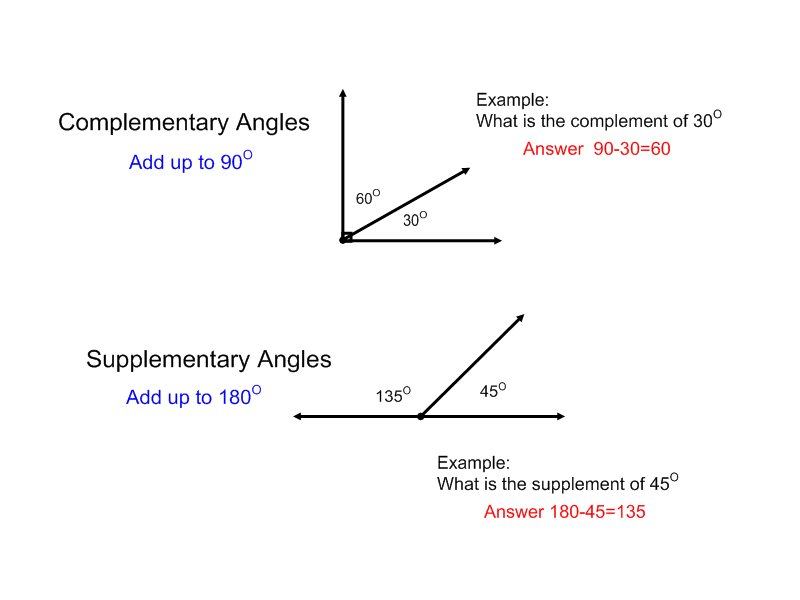
  Complementary Supplementary Angles

---

  Metric Unit Conversion Worksheet

---

  Area Problem Solving Worksheets

---

What is the measure of an angle that is one-third the measure of its complement?

Let's denote the measure of the angle as x degrees and the measure of its complement as y degrees. Since the angle is one-third the measure of its complement, we have the equation x = (1/3)y. We also know that the sum of an angle and its complement is 90 degrees, so we have the equation x + y = 90. Now, substituting x = (1/3)y into x + y = 90 gives us (1/3)y + y = 90, which simplifies to (4/3)y = 90. Solving for y, we get y = 67.5 degrees. Finally, substituting y = 67.5 into x = (1/3)y gives us x = (1/3)(67.5) = 22.5 degrees. Therefore, the angle measures 22.5 degrees.

Two angles are complementary. If one of them is twice the measure of the other, what are their measures?

Let x be the measure of the smaller angle. Since the larger angle is twice the measure of the smaller angle, it would be 2x. Since the two angles are complementary, their sum is equal to 90 degrees. Therefore, x + 2x = 90. Simplifying the equation gives 3x = 90, which implies x = 30. Thus, the smaller angle measures 30 degrees and the larger angle measures 2(30) = 60 degrees.

Find the measure of each angle if the measure of the complement of an angle is 30 degrees more than the angle itself.

Let the measure of the angle be x degrees. Since the complement of an angle adds up to 90 degrees, the complement of the angle is 90 - x degrees. Given that the complement of the angle is 30 degrees more than the angle itself, we can set up the equation: 90 - x = x + 30. Solving for x gives x = 30. Therefore, the angle is 30 degrees and its complement is 60 degrees.

Two angles are supplementary. If one angle measures 75 degrees, what is the measure of the other angle?

If two angles are supplementary, their measures add up to 180 degrees. So, if one angle measures 75 degrees, the measure of the other angle would be 180 degrees - 75 degrees = 105 degrees.

Find the measure of an angle if its supplement is four times the measure of its complement.

Let the measure of the angle be x degrees. Its supplement would be 180 - x degrees and its complement would be 90 - x degrees. Given that the supplement is four times the measure of its complement, we can write the equation: 180 - x = 4(90 - x). Simplifying this equation, we get x = 30 degrees. Therefore, the measure of the angle is 30 degrees.

Two angles are complementary. If the measure of one angle is 45 degrees, what is the measure of the other angle?

Since two angles are complementary, their measures add up to 90 degrees. If one angle is 45 degrees, then the other angle would be 90 degrees - 45 degrees = 45 degrees. Thus, the measure of the other angle is 45 degrees.

The measure of one angle is 30 degrees more than twice the measure of another angle. Find the measures of both angles.

Let x be the measure of the smaller angle. According to the given information, the larger angle is 30 + 2x degrees. Therefore, the sum of the two angles is x + (30 + 2x) = 3x + 30 degrees. Since the sum of the angles in a triangle is 180 degrees, we have 3x + 30 = 180. Solving for x, we find x = 50 degrees. Therefore, the smaller angle is 50 degrees and the larger angle is 30 + 2(50) = 130 degrees.

If the measure of one angle is 45 degrees, what is the measure of its supplement?

The measure of the supplement of an angle is 135 degrees. This is because the supplement of an angle is always 180 degrees minus the measure of the angle, so for an angle measuring 45 degrees, its supplement will be 180 - 45 = 135 degrees.

The measure of one angle is three times the measure of another angle. If their sum is 120 degrees, what are the measures of the angles?

Let the measure of the smaller angle be x degrees. The larger angle is then 3x degrees. Since their sum is 120 degrees, we have x + 3x = 120, which simplifies to 4x = 120. Dividing both sides by 4 gives x = 30. Therefore, the smaller angle is 30 degrees and the larger angle is 3(30) = 90 degrees.

The measure of one angle is four times the measure of another angle. If their sum is 160 degrees, what are the measures of the angles?

Let the measure of the smaller angle be x degrees. Therefore, the measure of the larger angle is 4x degrees. Given that their sum is 160 degrees, we can set up the equation x + 4x = 160. Solving this equation gives us x = 32 degrees for the smaller angle, and 4x = 128 degrees for the larger angle. Hence, the measures of the angles are 32 degrees and 128 degrees, respectively.