Algebraic Expressions Worksheets On Math
Algebraic expressions worksheets provide a structured and comprehensive way for students to practice and enhance their understanding of mathematical concepts related to algebra. These worksheets cater to individuals who are seeking additional resources to reinforce their learning in algebra and are looking for a practical way to solidify their knowledge. By completing these worksheets, students can become more proficient in simplifying and evaluating algebraic expressions, thereby building a strong foundation in mathematics.
Table of Images 👆
- Math Expressions Worksheets 7th Grade
- Simplify Expressions Worksheet
- Distributive Property and Combining Like Terms Worksheet
- 7 Grade Math Worksheets Algebraic Expressions
- 5th Grade Algebra Variables Worksheets
- Simplifying Quadratic Expressions Worksheets
- 7 Grade Math Worksheets Algebraic Expressions
- 6th Grade Math Worksheets Mean Median Mode
- Adding Polynomials Worksheet Printable
- Algebra Solving Linear Equations Worksheets
- Algebra Simplifying Fractions Worksheet
- 4th Grade Math Worksheets Fractions
- 6th-Grade Integers Worksheets
- 7th Grade Math Algebra Equations Worksheets
- These Basics for Algebra 1 Worksheets
- Multiplication Word Problems Worksheets
- Order Operations Problems
More Math Worksheets
Printable Math WorksheetsMath Worksheets Printable
Printable Math Worksheets Multiplication
Math Worksheets for 2nd Graders
Math Practice Worksheet Grade 6
Math Multiplication Worksheets
First Grade Subtraction Math Worksheets Printable
Rocket Math Practice Worksheets
Math Worksheets Integers
Superhero Math Worksheets
What are algebraic expressions?
Algebraic expressions are mathematical phrases that consist of variables, constants, and mathematical operations (such as addition, subtraction, multiplication, and division). They can be simple or complex and are often used to represent unknown quantities or relationships in equations. Examples of algebraic expressions include "3x + 4y" and "2a^2 - 5b + 7".
How do you simplify algebraic expressions?
To simplify algebraic expressions, combine like terms by adding or subtracting coefficients of the same variables. Use the distributive property to remove parentheses and then combine like terms. Look for opportunities to factor out common terms or use applicable rules, such as the associative or commutative properties. Finally, simplify any fractions or exponent rules if present in the expression. Keep applying these steps until the expression is in its simplest form.
What is the difference between a variable and a constant in an algebraic expression?
In an algebraic expression, a variable is a symbol that represents an unknown value or quantity that can change, while a constant is a value that remains the same throughout the expression. Variables can take on different values, whereas constants have fixed values that do not change.
How do you combine like terms in an algebraic expression?
To combine like terms in an algebraic expression, identify terms with the same variables raised to the same powers. Then, add or subtract their coefficients to simplify the expression. Remember to keep the variable terms unchanged and only work on the coefficients when combining like terms.
What is the purpose of using parentheses in algebraic expressions?
Parentheses in algebraic expressions are used to specify the order in which the operations need to be performed. They help clarify the hierarchy of operations and ensure that the expression is evaluated correctly. Parentheses indicate that the operations enclosed within them should be carried out first before proceeding with other calculations in the expression.
How do you evaluate an algebraic expression for a given value of the variable?
To evaluate an algebraic expression for a given value of the variable, you simply substitute the given value in place of the variable and simplify the expression. Replace any instances of the variable with the given value and perform the operations as needed, following the order of operations (parentheses, exponents, multiplication and division from left to right, and addition and subtraction from left to right) to get the final result of the expression for that specific value of the variable.
What are the basic operations in algebraic expressions (addition, subtraction, multiplication, division)?
The basic operations in algebraic expressions are addition, subtraction, multiplication, and division. These operations are used to combine, simplify, or manipulate algebraic terms and equations in order to solve for unknown variables or simplify expressions.
How do you write an algebraic expression to represent a word problem or a real-life situation?
To write an algebraic expression to represent a word problem or a real-life situation, first identify the unknown quantity or variable in the problem. Then, translate the given information into mathematical terms using symbols and operations. Make sure to clearly define what each variable represents in the context of the problem. Finally, simplify the expression if needed, ensuring that it accurately reflects the relationship between the quantities involved in the real-life situation.
What are the rules for multiplying and dividing algebraic expressions?
When multiplying algebraic expressions, you simply distribute each term in one expression by each term in the other expression and then combine like terms. When dividing algebraic expressions, you can simplify by factoring and canceling out common factors in the numerator and denominator. Remember that you cannot divide by zero, and be cautious when dealing with variables in denominators to avoid undefined values.
What are the steps to solving an equation involving algebraic expressions?
To solve an equation involving algebraic expressions, you first need to simplify both sides of the equation by combining like terms and performing any necessary operations. Then, isolate the variable you're solving for by performing the inverse operation (e.g., subtracting if the variable is being added, dividing if it's being multiplied). Repeat this process step-by-step until you have the variable isolated on one side of the equation and a numerical value on the other side. Finally, check your solution by substituting it back into the original equation and ensuring it satisfies the equation.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.








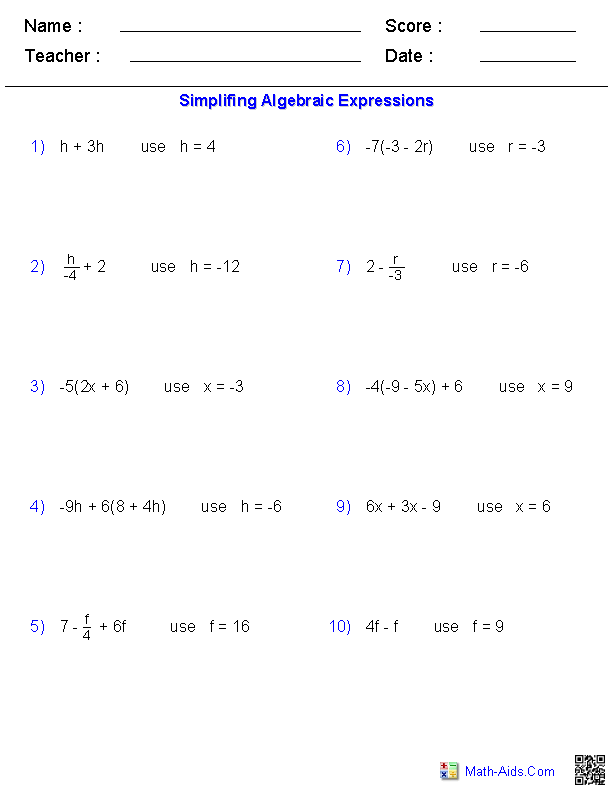





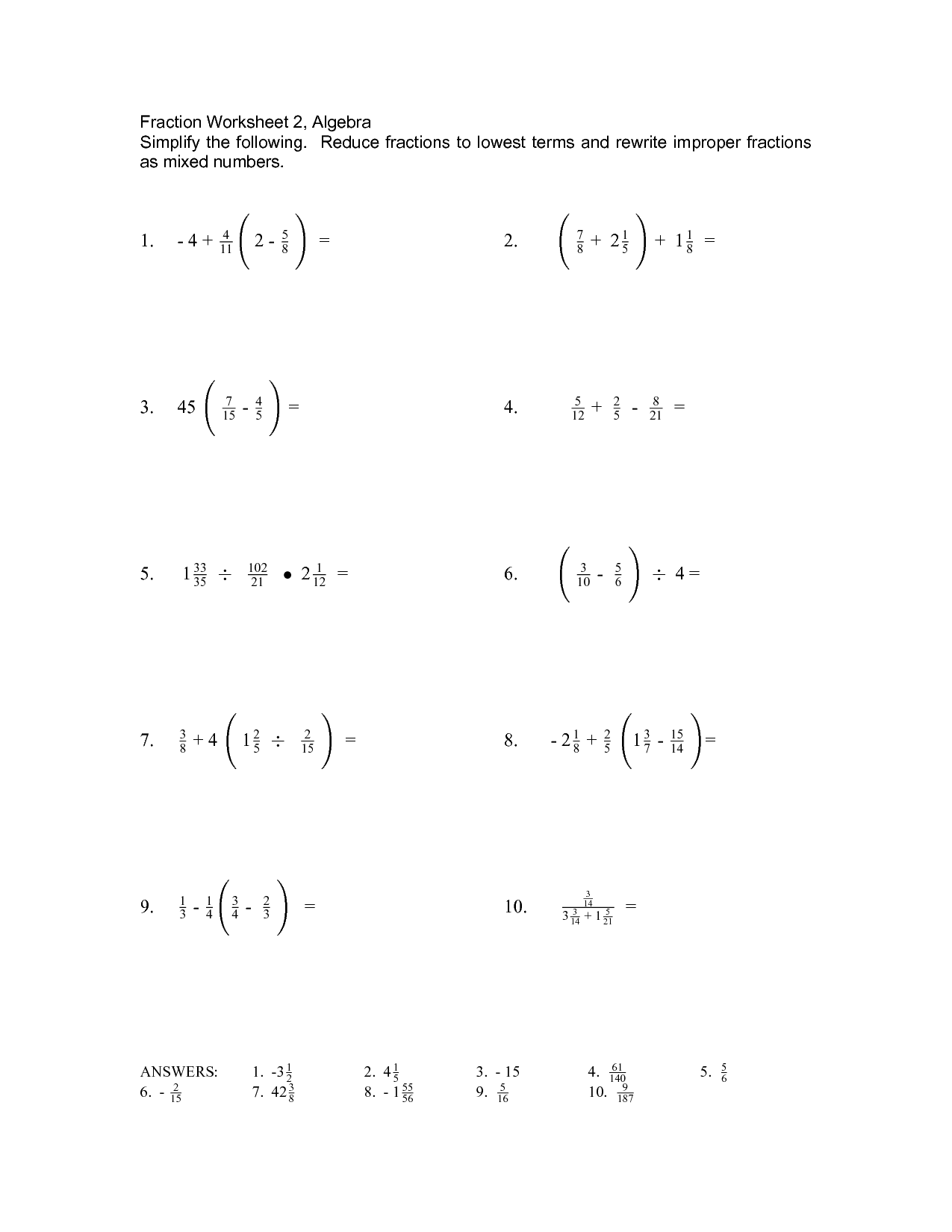




















Comments