Algebra Solving Inequalities Worksheet Key
The Algebra Solving Inequalities Worksheet Key offers a comprehensive solution guide for students who are seeking a clear and detailed understanding of solving inequalities in algebra. The worksheet key provides step-by-step explanations and example problems that cover the essential concepts and techniques necessary for mastering this topic. Whether you are a high school student, college student, or self-learner, this worksheet key serves as an indispensable resource to enhance your proficiency in solving inequalities.
Table of Images 👆
- Two-Step Inequalities Worksheets
- Graphing Linear Inequalities Worksheet
- Graphing Quadratic Equations Worksheet
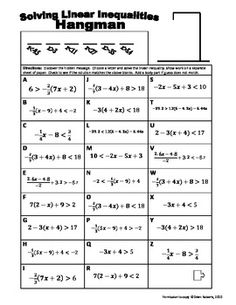
- Solving Linear Inequalities Hangman Key
- Quadratic Formula Worksheet
- Writing Equations Kuta Software Infinite Algebra 1 Answers
- Multi-Step Equations Worksheets
- Exponential and Logarithmic Equations Worksheet
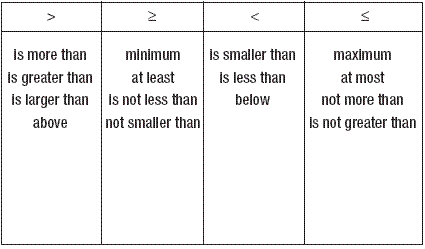
- At Least Inequality Symbol
- 6th Grade Math Worksheets Mean Median Mode
- Graphing Linear Equations Using Tables Worksheet
- Linear Equations Slope-Intercept Worksheets
- Literal Equations Worksheet with Answers
- Literal Equations Worksheet with Answers
- Literal Equations Worksheet with Answers
- Literal Equations Worksheet with Answers
More Other Worksheets
Kindergarten Worksheet My RoomSpanish Verb Worksheets
Healthy Eating Plate Printable Worksheet
Cooking Vocabulary Worksheet
My Shadow Worksheet
Large Printable Blank Pyramid Worksheet
Relationship Circles Worksheet
DNA Code Worksheet
Meiosis Worksheet Answer Key
Rosa Parks Worksheet Grade 1
What is the purpose of an inequality in algebra?
The purpose of an inequality in algebra is to express a relationship between two expressions that are not equal, but rather indicate a comparison of their values. Inequalities are used to show the relative sizes of numbers or expressions, allowing us to understand the relationships between quantities and make conclusions about their relative magnitudes.
What is the difference between solving an equation and solving an inequality?
The main difference between solving an equation and solving an inequality is that equations have an equals sign and require finding the value(s) that make the equation true, while inequalities use symbols such as < (less than), > (greater than), ≤ (less than or equal to), ≥ (greater than or equal to) and require finding the range of values that satisfy the inequality. In solving an equation, the goal is to find the exact solution(s) that make the equation balanced or equal, whereas in solving an inequality, the goal is to find the set of values that make the inequality statement true.
How do you graph an inequality on a number line?
To graph an inequality on a number line, first identify the boundary points by solving for the variable in the inequality. If the inequality is strict (< or >), use an open circle at the boundary points. If the inequality includes equality (≤ or ≥), use a closed circle at the boundary points. Then, shade the region on the number line that includes all the values that satisfy the inequality. If it is greater than or less than, shade above or below the line respectively. If it is greater than or equal to or less than or equal to, shade above or below the line including the boundary points.
What are the rules for adding or subtracting inequalities?
When adding or subtracting inequalities, you must keep the inequality sign the same if you are adding or subtracting the same value on both sides of the inequality. If you are adding or subtracting a negative value, you must reverse the inequality sign. Just be sure to follow these rules to maintain the validity of the inequality statement.
What happens to the direction of the inequality symbol when multiplying or dividing by a negative number?
When multiplying or dividing by a negative number, the direction of the inequality symbol flips. For example, if you multiply or divide both sides of an inequality by a negative number, the inequality sign changes direction. So, if you have "x > 5" and you multiply both sides by -1, it becomes "-x < -5".
How do you solve compound inequalities?
To solve compound inequalities, first solve each inequality separately. Then, identify the common solution set that satisfies all inequalities at the same time. Combine the individual solutions using the appropriate logical connective (either "and" or "or") depending on the given compound inequality. Finally, express the solution set in interval notation or set notation.
How can you solve absolute value inequalities?
To solve absolute value inequalities, first isolate the absolute value expression on one side of the inequality. Then, set up two separate inequalities, one without the absolute value signs for when the expression inside the absolute value is positive, and one with the expression inside the absolute value multiplied by -1 on the right side for when the expression inside the absolute value is negative. Solve each of these inequalities separately and determine the intersection of their solutions to find the final solution to the absolute value inequality.
What is the interval notation and how is it used to represent the solution set of an inequality?
Interval notation is a way to represent a set of real numbers using brackets and parentheses. In interval notation, round brackets ( ) indicate that the endpoint is not included in the set, while square brackets [ ] indicate that the endpoint is included. To represent the solution set of an inequality using interval notation, you would identify the range of values that satisfy the inequality and then express that range using appropriate combinations of brackets and parentheses to show whether the endpoints are included or excluded.
Can you solve an inequality with variables on both sides? If so, how?
Yes, you can solve an inequality with variables on both sides by rearranging the equation to isolate the variable on one side. You can do this by adding or subtracting terms from both sides of the inequality to simplify it and make the variable terms adjacent to each other. Then, you can solve for the variable by performing the necessary arithmetic operations and finding the value or range of values that satisfy the inequality.
How is solving systems of inequalities different from solving single-variable inequalities?
Solving systems of inequalities involves finding the intersection of the solution sets for each individual inequality in the system, while solving single-variable inequalities focuses on finding the set of values that satisfy the inequality for a single variable. In systems of inequalities, the solution is a region where the solution sets overlap, representing the values that satisfy all inequalities simultaneously. This contrasts with single-variable inequalities, where the solution is a specific range of values that satisfy the inequality for that single variable only.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.

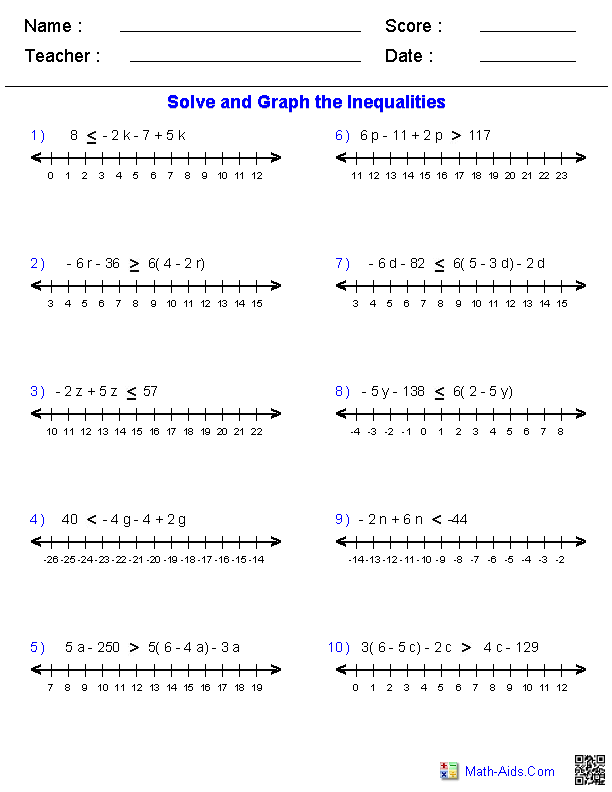








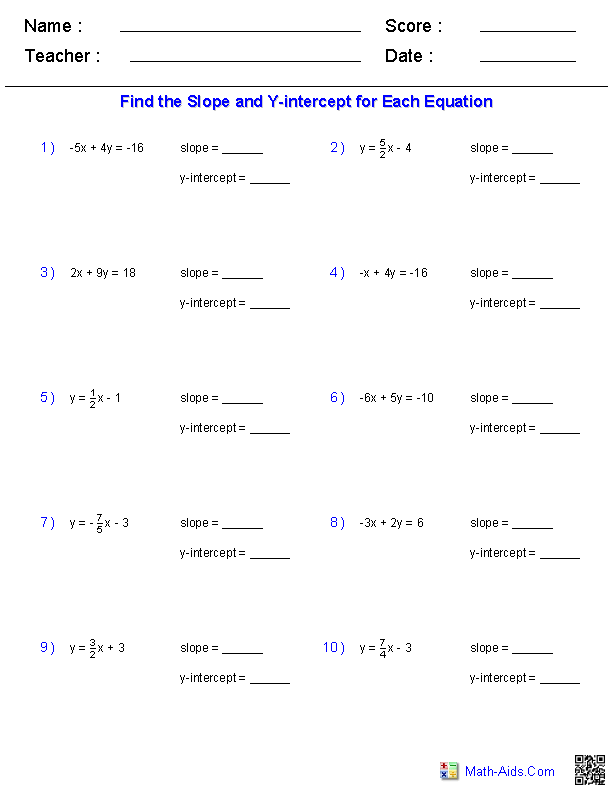


















Comments