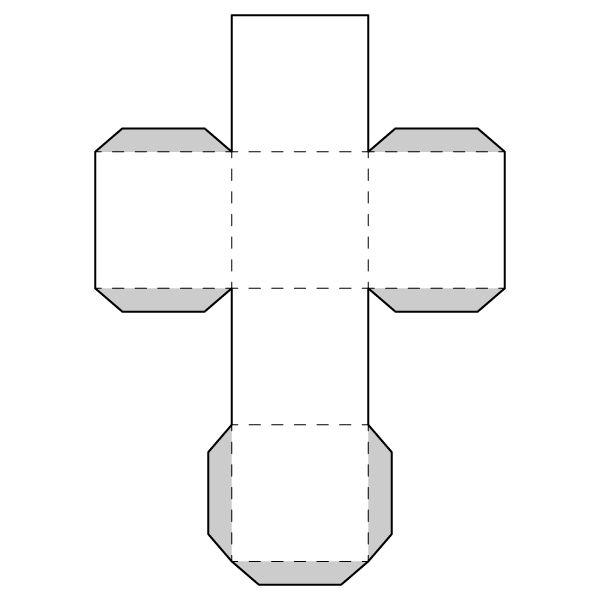
A Net of Cube Worksheet

Are you a math enthusiast or a teacher looking for engaging activities to reinforce 3D geometric concepts? If so, you'll love this comprehensive net of a cube worksheet. In this blog post, we'll explore the benefits of using worksheets as a powerful tool for teaching geometry, specifically the concept of nets, to students of different grade levels.

  Large Printable Cube Nets

---

  Cube Net Worksheet

---

  Fun Area and Perimeter Worksheets

---

  Surface Area Volume Cylinder Worksheet

---

  Surface Area and Volume Worksheets Grade 6

---

  3D Shape Nets Printable

---

  Rectangular Prism Volume Worksheet

---

  3D Shapes Triangular Prism

---

  Dice Cube Net

---

  Printable Number Dice Template

---

  Math Worksheets Multiplication Printable

---

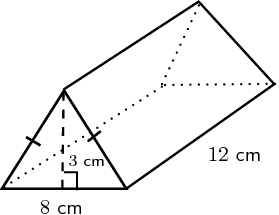
  Triangular Prism Surface Area Example

---

  White Plastic Laundry Basket

---

What is the purpose of A Net of Cube Worksheet?

The purpose of a net of a cube worksheet is to help students practice visualizing how a three-dimensional cube can be unfolded into a two-dimensional flat pattern. By cutting out the net and folding it, students can gain a better understanding of the faces, edges, and vertices of a cube, as well as enhance their spatial reasoning and geometry skills.

How many cubes are typically included in a net of a cube?

A net of a cube typically consists of six identical square faces, and therefore includes six individual cubes.

What is the shape of each face of a cube in the net?

Each face of a cube in its net is in the shape of a square, as a cube is made up of six equal square faces that are connected at their edges.

How are the edges of a cube represented in the net?

The edges of a cube are represented as lines connecting the vertices in the net of a cube. These lines show where the sides of the cube meet and intersect, giving a visual representation of the cube's shape when unfolded and laid flat.

Is it possible to create a net for a cube with irregular faces?

No, it is not possible to create a net for a cube with irregular faces. A cube by definition has six identical square faces that are all congruent and have equal side lengths. An irregular face would deviate from this definition, making it impossible to form a traditional net for a cube.

Can a net of a cube have more than six faces?

No, a net of a cube cannot have more than six faces because a cube has six faces, and the net of a cube is a two-dimensional representation that unfolds into these six faces. Any additional faces would not correspond to the actual shape of a cube.

How do the corresponding faces of a cube connect in the net?

In the net of a cube, the corresponding faces are connected along their edges to form a 3D cube when folded. Each face is attached to the adjacent face by their shared edges, allowing the net to be transformed into a cube by folding along these edges.

How can you determine the size and dimensions of a cube from its net?

To determine the size and dimensions of a cube from its net, you would need to look at the measurements of the different faces and edges shown on the net. By comparing the lengths and angles of the different sides and segments, you can calculate the dimensions of the cube. For example, if you know the length of one side of the square in the net, you can determine the length of each side of the cube since all sides are equal. Likewise, by analyzing the angles and relationships between different faces in the net, you can deduce the size and dimensions of the cube by applying geometric principles.

Are all the faces of a cube visible in its net?

Yes, all the faces of a cube are visible in its net. A net of a cube shows all six faces unfolded in a two-dimensional layout, providing a complete representation of the cube's surface area as if it were unrolled and laid flat.

What are some applications of working with nets of cubes in real life?

Working with nets of cubes has various applications in real life, such as in the fields of architecture and design for creating geometrically precise models and structures; in packaging and manufacturing for optimizing the use of materials and designing efficient packing solutions; in computer graphics and animation for creating 3D models and objects; in robotics for designing and programming robotic systems; and in education for teaching spatial reasoning and geometry concepts.