6th Grade Math Worksheets Exponents
If you're a math teacher or a parent of a 6th grade student who needs practice with exponents, you might be on the lookout for suitable worksheets to reinforce this important concept. Well, you've come to the right place! In this blog post, we will explore a variety of 6th grade math worksheets focused on exponents that will help students solidify their understanding of this mathematical entity and subject.
Table of Images 👆
- Exponents Worksheets
- Distributive Property 6th Grade Math Worksheet
- Exponents Worksheets
- 6th-Grade Exponents Worksheets
- Solving Equations Worksheets 7th Grade Math
- 8th Grade Math Problems Worksheets
- Powers and Exponents Worksheet
- Negative Exponents Algebra 1 Worksheets
- Simplify Expressions Worksheet
- Order of Operations PEMDAS Worksheets 6th Grade
- Printable 6th Grade Exponents Worksheets
- Simplifying Radicals Worksheet
- 7th Grade Math Worksheets Algebra
More Math Worksheets
Printable Math WorksheetsMath Worksheets Printable
Printable Math Worksheets Multiplication
Math Worksheets for 2nd Graders
Math Practice Worksheet Grade 6
Math Multiplication Worksheets
First Grade Subtraction Math Worksheets Printable
Rocket Math Practice Worksheets
Math Worksheets Integers
Superhero Math Worksheets
What is an exponent?
An exponent is a mathematical notation that indicates the number of times a base number is multiplied by itself. It is represented as a small raised number to the right of the base number, such as in 2^3, where 2 is the base and 3 is the exponent, meaning 2 is multiplied by itself 3 times (2*2*2=8).
How do you read an exponent expression?
To read an exponent expression, you typically start by saying the base (the number being raised to a power), followed by the word "raised to the power of" or "to the exponent". Then you say the exponent (the small number written above and to the right of the base). For example, for the expression 2^3, you would read it as "2 raised to the power of 3" or "2 to the third power.
How do you simplify expressions with exponents?
To simplify expressions with exponents, you can use the properties of exponents, like the product rule (a^m * a^n = a^(m+n)), the quotient rule (a^m / a^n = a^(m-n)), and the power rule ((a^m)^n = a^(m*n)). Additionally, remember that any number raised to the power of 0 is 1 and any number raised to the power of 1 is the number itself. These rules will help you combine like terms, reduce the exponents and simplify the expression efficiently.
What is the difference between a base and an exponent?
A base is the number that is being raised to a power in an exponential expression, while the exponent is the small number that indicates how many times the base is multiplied by itself. In other words, the base is the number being operated on, and the exponent represents the number of times that base is multiplied by itself.
How do you multiply numbers with exponents?
To multiply numbers with exponents, you simply add the exponents if the bases are the same. For example, when multiplying numbers like 2^3 * 2^2, since the bases are the same (2), you add the exponents (3 + 2) to get 2^5. This rule applies to all numbers with the same base.
How do you divide numbers with exponents?
To divide numbers with exponents, you subtract the exponents of the same base. For example, to divide \( x^a\) by \(x^b\), you subtract b from a, resulting in \(x^{a-b}\). This property applies to any base, not just x.
What is the rule for raising a power to a power?
When raising a power to a power, you simply multiply the exponents. This means that (a^m)^n is equal to a^(m*n), where "a" is the base and "m" and "n" are the exponents.
How do you evaluate expressions with negative exponents?
To evaluate expressions with negative exponents, you can move the term with the negative exponent to the opposite side of the fraction bar, which will convert the negative exponent to a positive one. For example, if you have 2^-3, you can write it as 1/2^3, which simplifies to 1/8. Alternatively, you can also rewrite negative exponents as fractions with positive exponents by taking the reciprocal of the base raised to the positive exponent.
How do you simplify expressions with zero exponents?
To simplify expressions with zero exponents, you can simply represent any base raised to the power of zero as equal to 1. This means that any term with a zero exponent in the expression can be replaced with a 1, effectively simplifying the overall expression. Remember that any number raised to the power of zero is always equal to 1, regardless of the base.
How do you solve word problems involving exponents?
To solve word problems involving exponents, first, you need to understand the relationship between the base number and the exponent. Identify the base number and the exponent in the problem, then apply the appropriate exponent rule (such as multiplication, division, power of a power) to simplify the expression. Remember to follow the order of operations (PEMDAS) to solve the problem step by step. It's also helpful to write out the problem and work through it systematically to ensure you don't make any mistakes.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.















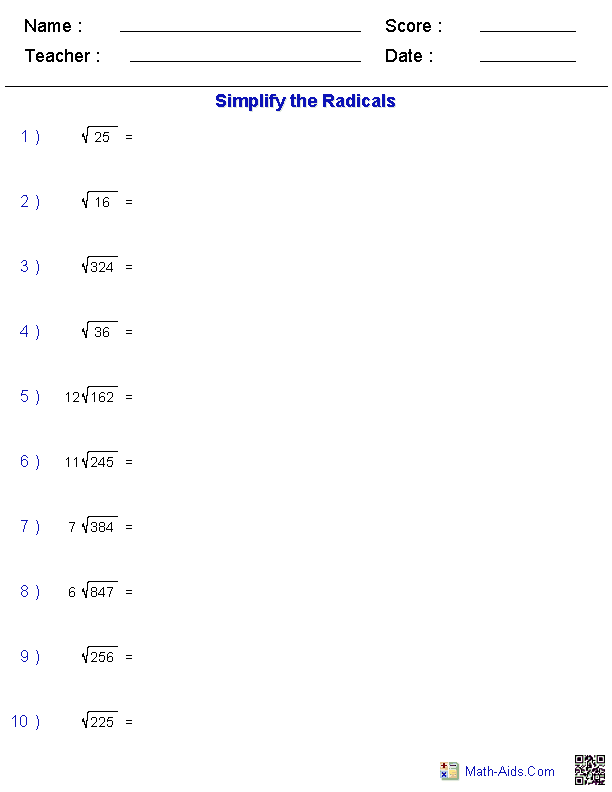















Comments